8. Tétel: Statisztika; Informatikai biztonság

Statisztikai minta és becslések, átlag és szórás.

Statisztikai minta:

• Statisztika:
  • Statisztika alatt a minta tömörítését értjük.
  • Célunk, hogy a mintában lévő információ minél nagyobb részét magyarázzuk a mintanagysághoz képest kevés számú mutatószámmal.
• Mivel a statisztikai sokaságot teljes körűen nem tudjuk megfigyelni, ezért annak egy részét vesszük abban a reményben, hogy annak megfigyeléséből vissza tudunk következtetni a teljes sokaságra.
• Minta alatt a statisztikai sokaság egy n elemű részhalmazát értjük, ahol véges sokaság esetén $1 <= n <= N$ (N az a természetes számok halmaza), végtelen sokaság esetén pedig n eleme természetes számok halmazának.
• A megfigyelt minta n darab valós szám.
• Mintavétel módszerei:
  • Egyszerű véletlen
  • Független azonos eloszlású
    • Visszatevéses
  • Szekvenciális
    • Sorozatos, folyamatos
  • Rétegzett
    • Férfi és nő választás
  • Csoportos

Statisztikai becslés:

• Egy adott minta alapján a sokaságra vonatkozóan állapít meg értékeket.
• A becsült érték valamennyire szinte mindig eltér a valódi értéktől.
• A becslés akkor jó, ha torzítatlan, egyik irányba sem elfogult.

Statisztika átlag:

• Összes adatot összeadjuk és elosztjuk annyival, ahány elemünk van.

Statisztika szórás:

• Átlagtól való eltérés.
• Az egyes számok átlagtól van eltérésének a négyzete, amit átlagolni kell, majd gyököt vonni.

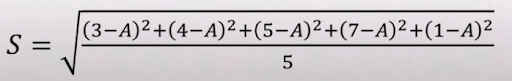
Konfidenciaintervallumok.

• Az intervallumbecslések egyik módszere a konfidenciaintervallum használata.
• Intervallum értékű becslést ad egy paraméterre, hogy valószínűleg ezen korlátok közé esik.
• Ez sok esetben jobb, mint egyetlen becsült értéket adni.
• Egy a paraméter egy előzetesen megadott értékére a becsült paraméter 1-a valószínűséggel esik az intervallumba.
• Ezt sokszor inkább százalékban adják meg.

Az u-próba.

• A populációból egy n elemszámú mintát veszünk, a minta értékeiből átlagot számolunk, majd meghatározzuk az átlag eltérését az m feltételezett populációs átlagtól.

• A kérdés, hogy az átlag és m különbség mértéke vajon: - Köszönhető-e a mintavétel véletlen hibájának - Vagy bizonyos p valószínűségű kockázatot vállalva utal-e arra, hogy a populációs átlag nem lehet m.

• Lépések:

  • Hipotézisvizsgálat, ahol
    1. Hipotézis megfogalmazása
    2. A próbafüggvény kiválasztása
    3. Kritikus és elfogadási tartomány
    4. Döntés

• Megfogalmazunk két egymásnak ellentmondó feltevést.

• Az egyik lesz a nullhipotézis (H0) a másik pedig az alternatív, vagy ellen hipotézis (H1).

• Ezt úgy kell megfogalmazni, hogy egymást kölcsönösen kizárják, így vagy egyiket vagy másikat kell elfogadni.

• Feltételezzük, hogy egy üdítőital gyárban minden üdítő 500ml-es.

• Tegyük fel azt, hogy a palackban 500ml-nél kevesebb üdítő van.

• Ezt az alternatívhipotézisben fogalmazzuk meg.

• H0-nak pedig tartalmaznia kell az egyenlőségjelet, és a fennmaradó részt.

• Hipotézisvizsgálat eredménye az, hogy a hipotézis mennyire hihető, nem azt adja meg, hogy az állítás igaz vagy hamis.

• Ennek a tesztelésére szolgáló eljárásokat nevezzük statisztikai próbáknak.

• Próbafüggvény egy konkrét minta alapján lehetővé teszi a hipotézis helyességének ellenőrzését.

• U-próba próbastatisztikája:

  • $x$ vizsgált valószínűségi változó átlaga
  • $m$ az előre adott érték, amihez az átlagot viszonyítjuk
  • $o$ a vizsgált valószínűségi változó ismert szórása
  • $n$ a minta elemszáma

• Kritikus tartományok és elfogadási tartományok:

  • $H0$ eldöntése céljából.
  • Elfogadási tartományt úgy választjuk meg, hogy a nullhipotézis fennállása esetén a próbafüggvény előre megadott nagy valószínűséggel ebbe a tartományba essen.

• Döntés:

  • Ha a mintavétellel kapott eredményünk szerint a próbafüggvény az elfogadási tartományba esik, akkor a $H0$ hipotézist megtartjuk, ezt tekintjük igaznak, a $H1$-et pedig elvetjük.

---

Az informatikai biztonság fogalma, legfontosabb biztonsági célok.

Az infobiztonság fogalma:

• A rendszerben kezelt adatok bizalmassága, sértetlensége és rendelkezésre állása, illetve a rendszerelemek sértetlensége és rendelkezésre állása szempontjából zárt, teljes körű, folytonos és kockázatokkal arányos.

Legfontosabb biztonsági célok:

• CIA

  • Bizalmasság (Confidentiality):
    • Titkos vagy személyes információk nem kerülhetnek jogosulatlanok kezébe.
    • A bizalmasságot az adatok tárolásánál, feldolgozásánál és továbbításánál is garantálni kell.
  • Sértetlenség (Integrity):
    • Adatintegritás:
      • Teljesülésekor az adat jogosulatlanul nem módosult tárolása, feldolgozása vagy küldése során.
    • Rendszer sértetlensége:
      • A rendszer működése az elvártnak megfelelő, jogosulatlan módosításoktól mentes.
  • Rendelkezésre állás (Availability):
    • Biztosítja, hogy a szolgáltatás az arra jogosultak számára a szükséges időben és időtartamra használható.

• Nyomon követhetőség:

  • Az a tulajdonság, hogy egy entitás által végrehajtott tevékenység visszakövethető legyen az entitáshoz.
  • A tevékenységek ellenőrzés céljára rögzítésre kerülnek azért, hogy visszakövethetőek legyenek, bizonyíték álljon rendelkezésre.
  • Ez a tulajdonság lehetővé teszi a letagadhatatlanságot, a behatolások megelőzését.

• Garancia, biztosíték:

  • A bizalom abban, hogy a négy másik biztonsági célt
  • (Bizalmasság, Sértetlenség, Rendelkezésre állás, Nyomon követhetőség) a biztonsági alrendszer megfelelően ellátja.

Fizikai, emberi, technikai fenyegetések és ellenük való védekezés.

Fizikai:

• Tűz
• Füst
• Víz
• Por
• Rovarok
• Penész

Emberi:

• Jogosulatlan fizikai hozzáférés
• Lopás
• Vandalizmus
• Visszaélés

Technikai:

• Feszültséghiány
• Túlfeszültség
• Elektromágneses interferencia

Fizikai védelem:

• Víz ellen vízérzékelő elhelyezése
• Por ellen ventilátor szűrő karbantartás.
• Nagyobb szervertermek hűtése a túlmelegedés ellen
• Tűz,füst tűzjelző, falak tűzállóak, légkondicionáló ne terjessze a tüzet, automata tűzoltó rendszer

Technikai védelem:

• Szünetmentes táp

Emberi védelem:

• Csak az arra jogosult léphet be
• Erőforrások zárt tárolóban való elhelyezése
• Berendezések rögzítése, a mozgathatóság megnehezítése érdekében
• Nyomkövető használata
• Megfigyelőrendszer
• Spamvédelem
• Letöltés korlátozása
• Gyakori védelmi tanfolyamok

Algoritmikus védelem eszközei: titkosítás, digitális aláírás, hash függvények.

Titkosítás:

• Az üzenetet szokás nyílt szövegnek (plain text) is nevezni.
• Az Adó az üzenetet nem az eredeti formájában küldi át a csatornán, hanem egy titkosító eljárásnak (encryption) veti alá.
• A csatornán tehát már nem a nyílt szöveg, hanem annak kódolt változata a titkos üzenet (ciphertext) megy át.
• Közvetlenül a Vevő sem tud mit kezdeni a titkos üzenettel, de ismerve a megfejtő, dekódoló eljárást (decryption) vissza tudja állítani az eredeti szöveget és értelmezni tudja azt.
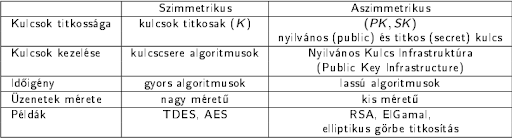
• 2 fajta:
  • Szimmetrikus
    • A kulcs közös, így azt mindkét félnek ismernie kell.
    • Gyors algoritmusok, nagy méretűek.
    • Pl: AES
  • Asszimetrikus
    • A kulcs különböző, mindkét fél rendelkezik egy kulcs párral (public, private).
    • A nyilvános kulcs mindenki számára elérhető, ez van a titkosításra.
    • A privát kulcs pedig a visszafejtésre.
    • Lassú algoritmusok, kis méretűek.
    • Nyilvános kulcsból a privát kulcs nem számolható ki.
    • Pl: RSA

Digitális aláírás:

• Az aláírt dokumentum igazolja az aláíró személyét vagy intézményét, valamint azt, hogy az adott személy/intézmény a dokumentum tartalmát ismeri, elfogadja, egyetért vele.
• Ezen kívül az aláírás igazolja, hogy a dokumentum tartalma nem változott meg, nem írtak bele új mondatokat és nem is töröltek belőle.
• A digitális aláírás az üzenethez csatlakozik, azaz az aláíró algoritmus hozzáfűzi az aláírást a konkrét elektronikus dokumentumhoz.
• Digitális aláírás érvényessége ellenőrző algoritmus futtatásával igazolható, mely bárki számára elérhető.
• Aláírás hamisítási szempontból a digitális aláírások sokkal megbízhatóbbak.
• Digitálisan aláírt dokumentum könnyen másolható és a másolat megegyezik az eredetivel.
• Egy megoldás speciális digitális aláírási rendszerek használata, a letagadhatatlan aláírások alkalmazása, mikor az aláírás ellenőrzéséhez az aláíró személy részvétele is szükséges.

Hash függvények:

• Tetszőleges véges hosszú üzenethez n hosszú üzenetet rendelünk.
• Adatintegritás ellenőrzése.
• Hash függvénnyel ellenőrizhetjük, hogy egy állomány változott-e vagy sem.
• Az állomány hash értéke szeparáltan tárolt.
• Kiszámítjuk az állomány hash értékét, és összevetjük a tárolt hash értékkel.
• Ha különböznek, akkor az állomány módosult.
• A hash értéket lenyomatnak is hívjuk.
• Lavinahatás:
  • Egy bit változása az inputban, jelentős változást eredményez az outputban.

Az AES és RSA algoritmusok.

AES:

• Egy módszer elektronikus adatok titkosítására.
• 4 x 4-es mátrixokat használ a titkosítás során.
• Blokkméret 128 bit, a kulcs pedig 128, 192, vagy 256 bit lehet.
• A kulcs méret meghatározása, hogy a bemeneti információt hány átalakítási ciklus éri, míg eléri a végleges titkosítási állapotát.
  • 10 ciklus 128 bites kulcs esetén.
  • 12 ciklus 192 bites kulcs esetén.
  • 14 ciklus 256 bites kulcs esetén.
• Minden ciklus számos lépést foglal magába, ezek között van az a lépés is, ami alapján a kulcs a mátrixot módosítja.
• Visszaalakítás során ugyanennyi ellentétes ciklust hajtanak végre a kulcs segítségével.
• Lépései:
  1. Tényleges kulcsok előállítása a nyers kulcsból.
  2. Előkészítés
     • A mátrix minden bájtját kizáró vagy művelettel módosítják a tényleges kulcs segítségével.
  3. Ciklusonként ismétlődő lépések:
     1. Minden bájtot a state mátrixban lecserélnek egy 8 bites helyettesítési táblára.
        • SubBytes
     2. Mátrix sorainak módosítása, körkörös eltolással.
        • ShiftRow
     3. Szubkulcs kombinálása a state mátrixxal.
        • AddRoundKey
     4. Oszlopok mind a 4 bájtját módosítják.
        • MixColumn
  4. Utolsó ciklus
     • Kimarad a MixColumn.

RSA:

1. Válasszunk két nagy prímet, mondjuk $p$-t és $q$-t.
   • Miller-Rabin teszttel gyorsan eldönthető, hogy prím szám-e.
2. Majd számoljuk ki az $N = p * q$-t.
3. Majd számoljuk ki az Euler féle $fi$ függvényt $N$-re, ami:
   • $fi(N) = (p-1)(q-1)$
4. Válasszunk egy olyan egész számot, $e$-t, melyre teljesül:
   • Egynél nagyobb, de $fi(N)$-nél kisebb
   • Majd $e$ és $fi(N)$ legnagyobb közös osztója $1$.
     • $lnko(e,fi(N)) = 1$
   • Majd $e$-t nyilvánosságra hozzuk.
5. Számítsuk ki $d$-t:
   • $d$-t titkokban tartjuk, mint a titkos kulcs kitevője.

Titkos kulcs: - $N$ modulusból és a $d$ kitevőből áll. - Vagy $N$ modulusból, $d$ kitevőből, és $n$ és $q$ prímekből.

Nyilvános kulcs: - $N$ modulusból és az $e$ kitevőből áll.

Üzenet kódolása:

• A elküldi a nyilvános kulcsát $B$-nek.
• Majd $B$ elküldené az üzenetét ($M$) $A$-nak.
  • Ehhez $M$-et darabolja úgy, hogy a kapott értékre igaz legyen, hogy kisebb, mint $N$.
  • Majd kiszámolja a titkos üzenetet.
    • $c = me mod N$

Visszafejtése:

• A ezután saját titkos kulcsát használva visszafejti $m$-et $c$-ből.
  • $m = cd mod N$

További információk