7. Tétel: Lineáris egyenletrendszerek; Automaták II

Lineáris egyenletrendszer fogalma és megoldása Gauss eliminációval.

Lineáris egyenletrendszer fogalma:

Olyan többismeretlenes egyenletrendszer, ahol minden ismeretlen első hatványon szerepel.

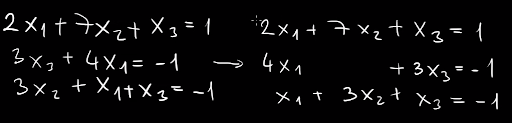
Megoldása Gauss-eliminációval:

• Az egyenletrendszert felírjuk egy mátrix alakként, ő lesz az együtthatómátrix.
• Az együtthatómátrix mellé felírom az egyenlőségjel jobb oldalán található értékeket.

• Ahol mindegyik sor egy egyenlet.
• A cél, egy felső háromszögmátrix kialakítása.
• A sorok felcserélhetőek, a cél, hogy a főátló alatt minden szám 0 legyen.
• A sorok kivonhatóak egymásból vagy éppen összeadhatóak és egy sor szorozható annak érdekében, hogy elérjük a várt eredményt.
  • (főátló alatt minden 0 legyen)
• Így, ha kijött a várt eredmény, az x3 értéke kiszámolható.

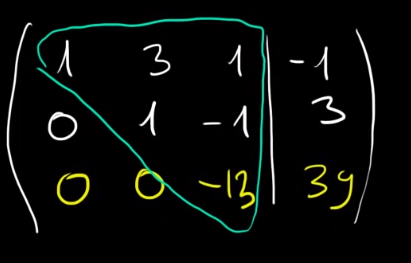
• Ebből a többi x értéke is kiszámolható.

---

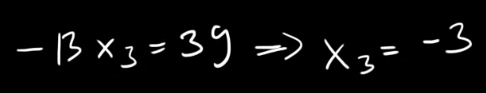
Determinisztikus Turing-gépek, lineárisan korlátozott automaták, eldönthetetlen problémák, tár és idő korlátok.

Determinisztikus Turing-gép:

• Először a legegyszerűbb változatát definiáljuk a Turing-gépnek, az egyszalagos Turing-gépet.
  • Ekkor a gépnek egyetlen szalagja van, egy író-olvasó fejjel, mely mindkét irányba tud mozogni a szalagon.
• A gép kezdetben a q0 állapotban van, a szalag elején a bemeneti szó található a szalag többi része szimbólumokkal van feltöltve és a fej a szalag első (bal szélső) mezőjén áll.
  • Ez a gép kezdő helyzete.
• A gép minden lépésben beolvassa a szalagon az aktuális karaktert, majd ennek, és az eddigi állapotnak a hatására változik az állapota, módosíthatja az író-olvasó fej alatt látott karaktert, majd lép a szalagon egyet jobbra vagy balra, esetleg helyben marad.
• Az átmeneti függvény azt írja le, hogy egy lépés során mit tesz a gép megadhatja, hogy ha a gép q állapotban van, a betűt olvas a szalagról akkor q' állapotba kerül, az olvasott a-t felülírja b-vel, majd a szalagot olvasó és író fej D irányba lép.
• A Turing-gép egy számítás során a kezdőhelyzetből indulva az átmeneti függvénynek megfelelő lépések sorozatát hajtja végre.
• Ha a szalag elején balra lépne, akkor a gép hibával megáll.
• Egyébként a működés akkor ér véget, ha nem tud lépni, elakad, mert az adott belső állapotra nincs értelmezve a függvény.
• A gép akkor fogadja el a bemeneti szót, ha ez az elakadás F-beli állapotban történik.
• Használat közben előfordulhat, hogy a Turing-gép:
  • Leáll elfogadó állapotban
  • Leáll hibával
  • Leáll nem elfogadó állapotban
  • A gép sosem áll le a bemenet hatására.
• Turing-gép egy rendezett hetes:
  • $Q$ belső állapotok véges halmaza
  • $q0$ kezdőállapot
  • $V$ szalagábécé
  • $T$ inputábécé (T eleme V-nek)
  • # szóköz betű
  • $F$ végállapotok halmaza
  • $d$ gép mozgásfüggvénye (bal, jobb)

Lineárisan korlátozott automata:

• Környezetfüggő nyelveket fogadja el.
• Az automata egy véges vezérlővel rendelkezik és egy szalaggal, amelyen kezdetben az input szó áll.
• Az automata a működése során két lényeges eltérést mutat az eddig tárgyalt automatákhoz képest:
  • Az egyik, hogy a szalagon a fej előre és hátra is mozoghat
  • A másik, még lényegesebb, hogy nem csak olvashatja a szalagot, de annak tartalmát át is írhatja, ennek megfelelően nem olvasó, hanem író-olvasó fejről beszélünk.
• 7 részből áll:
  • $Q$ belső állapotok véges halmaza
  • $q0$ kezdőállapot
  • $V$ szalagábécé
  • $T$ inputábécé (T eleme V-nek)
  • # speciális jel
  • $F$ végállapotok halmaza
  • $d$ gép mozgásfüggvénye (bal, jobb, helyben)
• Akkor mondjuk, hogy az automata elfogadja az input szót, ha végállapotba jut.
• # (speciális jelek) nem írhatóak felül.
• Az automata csak az eredeti input által elfoglalt területet használhatja számolásra.

Eldönthetetlen problémák:

• Egy probléma eldönthetetlen, ha nincs egyáltalán őt eldöntő algoritmus.

Tár és idő korlátok:

• Néhány feladat megoldhatósága messze lehet a gyakorlati megoldhatóságtól.
• Egy Turing-gép időigénye az a time függvény, mely a gép lépésszámának maximumát adja meg n hosszúságú bemenet esetén.
• Tegyük fel, hogy a gépnek el kell olvasnia minden bemenetet:
  • Ekkor a space tárigény függvény úgy definiáljuk, mint a gép szalagjain azon különböző mezők maximális számát az n hosszúságú bemenetek esetén, melyekre a gép ír.

Nemdeterminisztikus Turing-gépek, nevezetes nyelvosztályok, P, NP.

Nemdeterminisztikus Turing-gép:

• A fő különbség a determinisztikus változathoz képest tehát az, hogy most egy állapot és egy olvasott karakter hatására többféle műveletet is végezhet a Turing-gép.
• Ellentétben a véges automatával és a veremautomatával, a nemdeterminisztikus Turing-gép esetén nem kell külön átmenetekkel bajlódnunk.
• Ha meg akarjuk engedni, hogy a gép léphessen úgy, hogy a fej alatt álló karaktert nem olvassa el, akkor ezt megtehetjük egy olyan szabálycsoport létrehozásával, melyben a fej bármit is olvas, ugyanazt írja vissza és a fej helyben marad.
• Egy adott bemeneti szó esetén a gép lehetséges számításait egy úgynevezett számítási fával is leírhatjuk.
• A fa gyökere a kezdőállapot, csúcsai a gép állapotai, elágazása pedig az adott állapotban lehetséges lépések.
• Akkor fogadja el az állapotát, ha a fában van elfogadó levél, és a belső állapota elfogadó.

Nevezetes nyelvosztályok:

• A determinisztikus Turing-gép akkor fogad el egy inputot, ha azzal indítva leáll.
• A nemdeterminisztikus Turing-gép ugyanannál az inputnál más és más lépést sorozatokat hajthat végre, egyes esetekben megáll, máskor pedig nem.
• PSPACE:
  • Determinisztikus Turing-géppel polinomiális időben kiszámolható problémák osztálya.
• NPSPACE:
  • Nemdeterminisztikus Turing-géppel polinomiális időben kiszámolható problémák osztálya.
• A PSPACE és NPSPACE problémaosztály egybeesik.

További információk