6. Tétel: Gráfok; Automaták I

Gráf fogalma és megadásának módjai.

Gráf fogalma:

• Gráfnak nevezzük pontoknak és éleknek a halmazát, ahol az élek pontokat kötnek össze, illetve az élekre pontok illeszkednek úgy, hogy minden élre legalább egy, legfeljebb két pont illeszkedik.
• A gráfok pontjait egyszerűen pontoknak, vagy csúcspontoknak, vagy csúcsoknak nevezzük. A gráf pontjait nagy betűkkel, az éleit kis betűkkel jelöljük.
• Hálós adatszerkezet.

Egyszerű, irányított és irányítatlan gráfok.

Egyszerű gráf:

• Egy gráf egyszerű, ha nincs benne sem többszörös él, sem hurokél.

Irányított gráf:

• Az éleknek irányuk van, végpontok között nincs különbség.

Irányítatlan gráf:

• Az éleknek nincs irány elrendelve, vagyis nem teszünk különbséget A-ból B-be, illetve B-ből A-ba menő élek között.

Séta, út, összefüggőség.

Gráf összefüggő:

• Ha bármelyik csúcsából el lehet jutni másik csúcsba élek mentén.

Út:

• Élek olyan sorozata, melyben nem ismétlünk sem éleket, sem csúcsokat.

Séta:

• Egy séta csúcsok és élek váltakozó sorozata, mely csúccsal kezdődik és csúcsban végződik..

Gráffal végezhető műveletek:

• Létrehozás
  • Üres gráfot hozunk létre
• Bővítés
  • Az új elem értéke mellett meg kell adni a megelőzőinek és a rákövetkezőinek a listáját is.
• Törlés
  • fizikai
• Csere
• Rendezés
• Keresés, elérés, feldolgozás
• Bejárás
  • Szélességi vagy mélységi

Szélességi bejárás:

• A bejárás során az adatelemeket fehér, szürke és fekete színűre fogjuk színezni, valamint egy sort fogunk használni a szürke színű adatelemek tárolására.
• A bejárás során a feldolgozott elemekből feszítőfákat építünk fel.

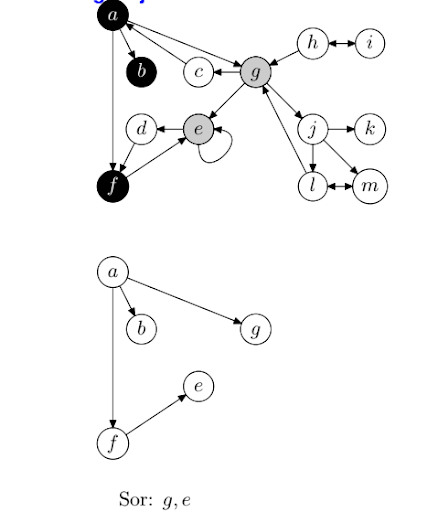
1. Színezzük a gráf adatelemeit fehér színűre és hozzuk létre az üres sort.
2. Ha minden adatelem fekete színű, a bejárás véget ér.
3. Ha a sor üres, válasszunk tetszőlegesen egy fehér színű elemet, színezzük szürkére, és helyezzük el a sorban. Ennek az elemnek a feldolgozásakor új feszítőfát fogunk elkezdeni építeni.
4. Ha a sorban van elem, vegyük ki a sor első elemét, fehér színű gyermekeit szürkére festve helyezzük el a sorban, majd az adatelemet fessük feketére, és helyezzük el a megfelelő feszítőfában.
5. Folytassuk az algoritmust a 2. lépéssel.

Mélységi bejárás:

• A bejárás során az adatelemeket fehér, szürke és fekete színűre fogjuk színezni, valamint egy vermet fogunk használni a szürke színű adatelemek tárolására
• A bejárás során a feldolgozott elemekből feszítőfákat építünk fel.

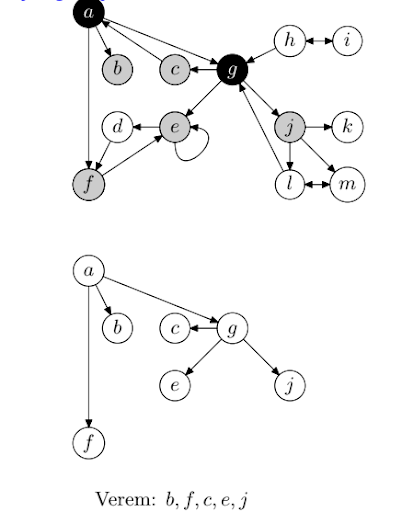
1. Színezzük a gráf adatelemeit fehér színűre és hozzuk létre az üres sort.
2. Ha minden adatelem fekete színű, a bejárás véget ér.
3. Ha a sor üres, válasszunk tetszőlegesen egy fehér színű elemet, színezzük szürkére, és helyezzük el a sorban. Ennek az elemnek a feldolgozásakor új feszítőfát fogunk elkezdeni építeni.
4. Ha a veremben van elem, vegyük ki a verem első elemét, fehér színű gyermekeit szürkére festve helyezzük el a veremben, majd az adatelemet fessük feketére, és helyezzük el a megfelelő feszítőfában.
5. Folytassuk az algoritmust a 2. lépéssel.

Nevezetes gráfok: páros gráf, teljes gráf, fa, kör, súlyozott gráf.

Páros gráf:

• Páros gráfnak nevezünk egy G gráfot, ha G csúcsainak halmazát fel tudjuk úgy osztani egy A és B halmazra, hogy az összes G-beli élre teljesül, hogy az egyik végpontja A-ban van, a másik pedig B-ben.

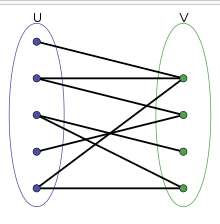
Teljes gráf:

• Egy olyan egyszerű gráf, amelynek minden csúcsa össze van kötve minden más csúccsal.

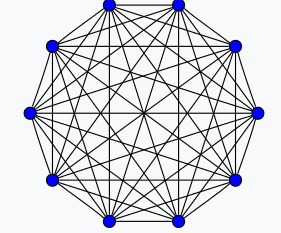
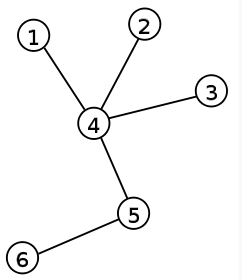
Fa:

• Fának nevezzük azokat a gráfokat, amelynek bármely két csúcsát pontosan egy út köti össze, azaz a fák körmentes összefüggő gráfok.

Kör:

• Körnek nevezzük azt az utat, amelynek kezdő és végpontja azonos, és az élek és pontok egynél többször nem szerepelhetnek.

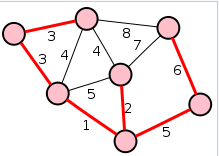
Súlyozott gráf:

• A gráf minden éléhez számértéket rendelünk, az él súlyát.
• Az élsúlyok legtöbbször valós számok.
• Egy út súlya az őt alkotó élek összsúlya.

---

Generatív nyelvtanok, nyelvosztályok, a Chomsky-hierarchia.

Generatív nyelvtan:

• Azon szabályok halmaza, amelyekkel minden, a nyelvben lehetséges jelsorozat előállítható, azaz leírja, hogyan lehet előállítani egy átírási eljárással a kitüntetett kezdő szimbólumból a többi jelsorozatot.

• A szabályokat egymás után kell alkalmazni a kezdő szimbólum átalakítására.

  • Pl:

• A $G = (N, T , S , H)$ rendezett négyest generatív nyelvtannak nevezzük, ha

  • $N$ és $T$ véges ábécék
  • $N$ elemei nemterminális jelnek nevezzük és nagybetűkkel jelöljük
  • $T$ elemei terminális jelnek nevezzük és általában kisbetűvel jelöljük
  • $H$ elemeit képző párokat helyettesítési szabályoknak nevezzük.
    • $p -> q$ jelöljük
  • $S$ a generálás kiinduló eleme

Nyelvtan osztályok, Chomsky-hierarchia:

• A formális nyelveket osztályokra osztja növekvő kifejezőerő szerint.
• Ez annyit jelent, hogy minden egymás után következő osztály előállíthatja a formális nyelvnek egy az előtt álló osztálynál tágabb csoportját.
• Type-0 (Kötetlen nyelvek)
  • Minden formális nyelvet magába foglal.
  • Ő generálja az összes nyelvet, amit a turing gép felismer.
• Type-1 (Környezetfüggő nyelvek)
  • Vannak szabályai, bal oldalán nem terminális áll stringekkel, jobb oldalán csak stringek
  • (a string terminálisokból és/vagy nem terminálisokból épül fel)
  • Azok a nyelvek, melyeket egy lineáris korlátozott automata felismer.
• Type-2 (Környezetfüggetlen nyelvek)
  • Szabályai, bal oldalán nem terminális, jobb oldalán string
  • (a string terminálisokból és/vagy nem terminálisokból épül fel)
  • Azok a nyelvek, melyeket egy nemdeterminisztikus automata felismer.
• Type-3 (Reguláris nyelvek)
  • Szabályai, bal oldalán nem terminális, jobb oldalán terminális, amit követhet egy nem terminális is.
  • Az összes nyelv, amit véges automatával el lehet dönteni.

Véges automaták, lineáris idejű felismerés, veremautomaták.

Automata:

• Egy olyan absztrakt rendszer, mely belső állapotait megadott szabályok szerint változtatja külső ingerek hatására.
• Az ingerekre adott válasz függ mind az ingerektől mind pedig a pillanatnyi belső állapottól.
• Ebben az értelemben tehát nemcsak a gépek, hanem bármiféle élő vagy élettelen objektumok tekinthetők automatának, ha ezen séma szerint vizsgáljuk őket.

Automata megadása:

• Egy automatát akkor tekintünk adottnak, ha a hozzá tartozó halmazok és függvények adottak.

Reguláris nyelv:

• Minden esetben egy formális nyelv
• Leírható reguláris kifejezések alkalmazásával.
• Elfogadja egy determinisztikus véges állapotú gép
• Elfogadja egy nemdeterminisztikus véges állapotú gép
• Elfogadja egy csak olvasó turing-gép

Nemdeterminisztikus automata:

• Egy véges állapotú gép, ahol bármelyik állapot-bejövő szimbólum párhoz több következő állapot is tartozhat.
• Nemdeterminisztikus kimenőjel nélküli automatának tekinthető a dobókocka, melynek egyetlen bemenő jele a feldobás.
• Ezen bemenő jel, azaz a feldobás hatására a dobókocka a hat lehetséges állapotából átmehet a hat lehetséges állapot bármelyikébe annak megfelelően, hogy a feldobás után éppen melyik lapjára esik.

Determinisztikus automata:

• Egy véges állapotú gép, ahol minden állapot-bejövő szimbólum párhoz egy és csakis egy másik állapotba való átmenet tartozik.

Lineáris idejű felismerés:

• A reguláris nyelvek esetén a szóprobléma nagyon hatékonyan megoldható.
• Ha megszerkesztünk egy az adott nyelvet elfogadó determinisztikus véges automatát, akkor annak segítségével a szót betűnként elolvasva végig követve az automata futását (legkésőbb) a szó végére érve megkapjuk a választ a kérdésre:
• ha végállapotba jutottunk a szó végén, akkor a szó benne van az adott reguláris nyelvben
• Ha nem végállapotba jutottunk, vagy (parciális automata esetén) időközben elakadtunk a feldolgozással, akkor a keresett szó nincs a nyelvben.
• Tehát a probléma valós időben megoldható, ahány betűből áll az input szó, annyi lépés után tudjuk a választ.

Veremautomaták:

• Ha a véges automata definíciójában az állapothalmaz végességére vonatkozó követelményt elhagyjuk, akkor végtelen automata fogalmához jutunk.
• A véges bemenő szót egy inputszalagon kapja meg.
• Ha az input szalagon egy nem üresszó van, és a veremautomata úgy áll meg a végállapotban, hogy előzőleg input szalag utolsó betűjét is beolvasta, akkor azt mondjuk, hogy a veremautomata az input szalagon lévő szót elfogadta.
• Veremautomata üres szót is elfogad, ha van olyan futásmódja, ami elfogadja.
• Veremautomata által elfogadott nyelvek osztálya épp a környezetfüggetlen nyelvek osztálya.
• Veremautomata alatt egy olyan rendezett hatost értünk, amiben szerepel a:
  • Állapotok halmaza (Q)
  • Kezdőállapot (q0)
  • Végállapotok halmaza (F)
  • Input ábécé (Σ)
  • Verem ábécé (Γ)
  • Átmenet függvény (δ)

További információk