5. Tétel: Mátrixok; Logikai problémák

Mátrix fogalma, műveletek, determináns, rang.

Mátrix:

• Egy m sorral és n oszloppal rendelkező számtáblázatot m x n-es mátrixnak nevezünk.
• Az összes m x n-es mátrix halmazát Mmxn-nel jelöljük.
• Ha n = m, akkor a mátrix négyzetes vagy kvadratikus.
• A mátrix főátlója alatt az (a11,a22,...amn) szám k-ast értjük.
• Két mátrix egyenlő, ha azonos típusúak (azaz ugyanannyi soruk és oszlopuk van), és a megfelelő elemeik megegyeznek.
• Azt az n x n-es mátrixot, melynek főátlójában csupa 1-es áll, minden más eleme 0, n-edrendű egységmátrixnak nevezzük.

Műveletek:

Mátrixok összeadása

-Csak azonos típusú mátrixokat tudunk összeadni. -Vagyis egy $n * k$-as mátrixhoz, csak egy másik $n * k$-as mátrixot tudunk hozzáadni. (sor és oszlopszám egyezik) -Azonos sor és oszlop-beli elemeket összeadjuk.

Mátrixok skalárral való szorzása

• Elemenként végezzük, azaz ha $λ ∈ R$, $A = (aij) ∈ Mmxn$, akkor $λ*A = (λaij) ∈ Mmxn$
• Mátrixot megszorozzuk egy számmal, vagyis a mátrix minden elemét megszorozzuk vele.

Mátrixszorzás

• Egy $n * k$-as mátrixszal csak egy $k * m$-es mátrixot szorozhatunk.
• Vagyis az a szorzásban szereplő első mátrix arra kell, hogy végződjön, amivel a következő kezdődik.
  • $(n * k)*(k * m) = (n * m)$
• Szorzat mátrixnak annyi sora lesz, mint $A$-nak és annyi oszlopa, mint $B$-nek.
• Elemei úgy keletkeznek, hogy $A$ egyik sorát szorozzuk $B$ egyik oszlopával.

Mátrixok inverze:

• Azt mondjuk az A n-edrendű négyzetes mátrixról, hogy létezik inverze, ha létezik olyan B n-edrendű négyzetes (kvadratikus) mátrix, hogy a szorzatuk egységmátrix.
• $A * A-1 = E$

Mátrixok determinánsa:

• Nem más, mint egy négyzetes mátrixhoz rendelt szám.
• 2x2 mátrix esetén:
  • Mátrix minden sorából és oszlopából kiválasztunk egy és csak egy elemet, majd ezeket összeszorozzuk.
  • Ezt az összes lehetséges módon megtesszük, majd ellátjuk egy előjellel.
• 3x3 mátrix esetén:
  • Kiszámolása saurrusz szabály néven ismert.
  • Fogjuk a mátrixot, majd saját maga mögé leírjuk még egyszer.
  • Majd vesszük a főátlókat és a mellékátlókat.
    • Főátlók elemeit összeszorozzuk és pozitív előjellel vesszük
    • A mellékátlók elemeit is összeszorozzuk, de azokat negatív előjellel vesszük.

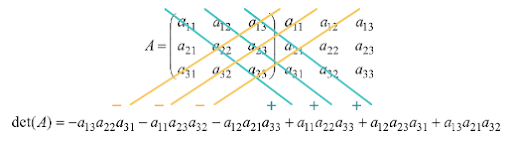
• Kifejtési tétel:
  • Minden n x n-es mátrixra jó.
  • Kifejtése sorok szerint történik.
    • Pl: vegyük az első sor elemeit, és alkalmazzuk rá a kifejtési tételt.
  • Váltakozó előjellel kell venni az elemeket.
    • Sakktábla szabályt megjegyezzük.
  • Vesszük az első elemet, leírjuk az adott előjellel, majd megszorozzuk az aldeterminánssal, és így tovább..
  • Aldeterminánsok pedig úgy keletkeznek, hogy az adott elem sorát és oszlopát egyszerűen kihúzzuk.
  • Ami marad, az lesz az aldetermináns
  • Az aldeterminánsokat pedig 2 x 2 mátrixok determinánsaként kiszámoljuk.

• Gauss-elimináció:

  • A mátrixot felső háromszög alakúra hozzuk (főátló alatt csupa 0), ekkor a determináns éppen a főátlóbeli elemek szorzata.

• Mátrix rangja:

  • Mátrixot a Gauss-elimináció segítségével alakítjuk át ekvivalens mátrixba.
  • Átalakítás után a nemnulla együtthatókkal rendelkező sorvektorok száma megfelel a mátrix rangjának.

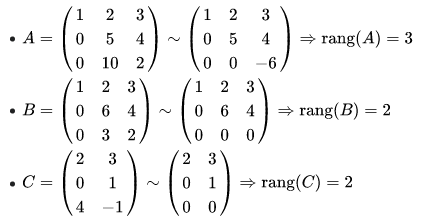
Speciális mátrixok, inverz.

Kvadratikus mátrix:

• Ugyanannyi sora van, mint oszlopa
• $(n * n)$

Diagonális mátrix:

• Olyan kvadratikus mátrix, aminek a főátlóján kívüli elemek nullák.

Egységmátrix:

• Olyan diagonális mátrix, amelynek minden főátló-eleme egy.

Inverz mátrix:

• $A^{-1}$
• $A * A^{-1} = I$, vagyis az egységmátrix-szal.
  • Lehet:
    • Jobb inverz
      • $A * A^{-1} = I$
    • Bal inverz
      • $A^{-1} * A = I$

Transzponált:

• Sorokból oszlopot, oszlopokból sort gyárt.
• Jele: $A^{T}$ vagy $A*$
• Az olyan mátrixok, melyeknek transzponáltja önmaga, szimmetrikus mátrixoknak nevezzük.

Mátrix, mint lineáris transzformáció.

• Egy fí (Φ φ) lineáris leképezés egy lineáris transzformáció, ha $V1 = V2$.
• Egy lineáris transzformáció különböző bázisokra vonatkozó mátrixainak megegyezik a rangja és a determinánsa.

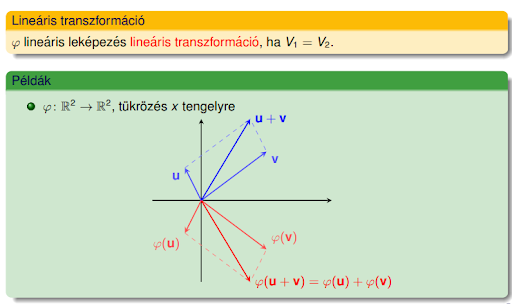
Sajátérték, sajátvektor.

Vektor:

• A számok egyfajta általánosításának is tekinthetőek.

Sajátvektor, sajátérték:

• Legyen A egy $n * n$-es mátrix.
• Az a $v$ nem nulla vektor, melyre igaz, hogy $A*v = λ*v$
• Ahol a $λ (lambda)$ valamilyen valós szám, és a $λ$ a saját értéke.

---

A problémaredukciós reprezentáció és az ÉS/VAGY gráfok

Problémaredukció:

• Egy adott problémát úgy próbálunk megoldani, hogy több külön-külön megoldandó részproblémára bontjuk.
• Ha a részproblémákat megoldjuk, az eredeti probléma megoldását is megkapjuk.
• A részproblémák megoldását további részek megoldására vezetjük vissza, egészen addig, amíg csupa olyan problémához nem jutunk, amelyeket egyszerűségüknél fogva már könnyedén meg tudunk oldani.

Problémaredukciós reprezentáció:

• Legyen $p$ egy probléma.
• Azt mondjuk, hogy a $p$ problémát problémaredukciós reprezentációval írtuk le, ha megadtuk a:
  • $〈P,p,E,R〉$ négyest, azaz
  • A megoldandó $p ∈ P$ problémát,
  • A $P$ nem üres halmazt, a $p$ problémához hasonló problémák halmazát
  • Az egyszerű problémák $E$ halmazát
  • A redukciós operátorok $R$ nemüres, véges halmazát

ÉS/VAGY gráf:

• Legyen a p probléma a $〈P,p,E,R〉$ reprezentációval megadva.
• Ez a reprezentáció is egy irányított gráfot, úgynevezett ÉS/VAGY gráfot határoz meg.
• A $P$ problémahalmaz elemei (a problémák) a gráf csúcsai.
  • Vezessük be a $q$ probléma által definiált csúcsra az $nq$ jelölést
    • Halmaza az $N$
• A gráf csúcsai közül kitüntetett szerepet játszanak a $p$ problémát szemléltető úgynevezett startcsúcs
  • Jele: $s$
• És az egyértelmű problémákat szemléltető terminális csúcsok.
  • Jele: $ne$
    • Halmaza a $T$
• Egy $q$ eleme $P$ problémát szemléltető csúcsból irányított éleket húzunk a problémákat szemléltető $nq$ csúcsokba.
• Ezek az élek összetartozónak tekinthetőek
  • Egy ÉS élköltséget vagy hiperélt alkotnak.
  • A gráf hiperéleinek halmaza az $E$
• Tehát azt mondjuk, hogy az $〈N,s,T,E〉$ irányított ÉS/VAGY gráf a p probléma $〈P,p,E,R〉$ problémaredukciós reprezentációjához tartozó reprezentációs gráfja.
• Az ÉS/VAGY gráfot olyan problémák reprezentálására alkalmazzuk, ahol a feladat felírható logikai állítások konjunkciójaként és diszjunkciójaként.
• Tehát a probléma végrehajtásánál a probléma szétválhat egy egy valamilyen formában eltérő problémára vagy alfeladatra (vagy kapcsolat), vagy egy adott probléma feladatot egyszerre kell megoldani (és kapcsolat).
• A gráfokkal további vizsgálatokat, átalakításokat vihetünk a feladatba, így könnyebben tudjuk elemezni a rendszerünket.

Ismeretreprezentációs technikák, bizonytalanság-kezelés (fuzzy logika).

Ismeretreprezentációs technikák:

Az ismeretreprezentáció azzal foglalkozik, hogy milyen eszközökkel lehet a tudás egy részét (az ismeretet) a számítógépen ábrázolni.

Reprezentáció szintjei:

1. Tudásszint
   • Valós világ tudati megjelenítése
   • Explicit tudás:
     • Közölt, szavakkal leírt
   • Implicit tudás:
     • Potenciálisan közölhető, leírható tudás
   • Rejtett, hallgatólagos tudás:
     • Nem közölhető, nem leírható
2. Szimbólikus szint
   • A tudás explicit vagy korábban közölt részeinek szimbólikus leírása
3. Technikai szint
   • A szimbólikus leírás számítógépes ábrázolása, algoritmusokkal, adatszerkezetekkel

Ismeretreprezentációs módszerek (Osztályozás szerint):

1. Osztály
   • Proceduláris (algoritmikus) reprezentáció
     • Stratégiát ad arra, hogy hogyan oldjuk meg a feladatot.
   • Dekleratív (leíró) reprezentáció
     • Csak azt írjuk le, mit kell megoldani
2. Osztály
   • Logikai reprezentáció
     • Struktúra nélküli dolgok leírására szolgál
   • Strukturált reprezentáció
     • Belső struktúrával rendelkező dolgok, objektumok és kapcsolataik leírására.
3. Osztály
   • Procedurális reprezentáció
     • Valamely programozási nyelven leírt vezérlést módosító eljárások
   • Logikai alapú reprezentáció
     • Szabályalapú reprezentáció
   • Strukturált reprezentáció
     • Asszociatív hálók, döntési fák, rokonsági hierarchiák
   • Hibrid reprezentáció
     • Többféle reprezentációt egyszerre támogató módszerek

Reprezentációs modellek:

• állapottér -reprezentáció
• Logikai reprezentáció
• Probléma redukció
• Elosztott reprezentáció
• Strukturált objektum alapú reprezentáció

Fuzzy logika:

• A fuzzy logika célja, hogy olyan módszerekkel szolgáljon, amelyekkel olyan problémák oldhatók meg, amelyek túlságosan bonyolultak, vagy nehezen megfogalmazhatóak a hagyományos vizsgálati módszerekkel.
• A logika formailag Arisztotelész tanításain alapul, ahol egy elem vagy tagja, vagy nem tagja egy halmaznak.
• Ha igen, akkor 1 (egy), ha nem akkor 0 (nulla) értéket vesz fel a logikai változó.
• Csak közelítő megoldás lehet.
• A 0 és 1 közötti értékek a bizonytalanságot reprezentálják.
• Alkalmazási technikái megtalálhatóak az automatizálási technikákban, üzemgazdaságban, orvosi technikában, szórakoztató elektronikában stb
• Tipikus alkalmazása a mosógépek oly módon történő programozása, hogy a gép a tisztítandó textíliák szennyezettségének függvényében adagolja a mosószert.
• A gondolatmenet kiindulópontja, hogy a ruhák szennyességi foka nem egyértelműen meghatározható. Példának okáért, nem létezik egy 55%-os szennyezettségi fok definíció.
• Mivel azonban a mosószer mennyisége pontosan meghatározandó, ezért egy olyan logikára van szükség, amely pontatlan, életlen fogalmakkal, mint "enyhén szennyes" vagy "erősen koszolódott" is bánni tud.
• Alapja a fuzzy halmazok (élettelen, elmosódott halmazok)
• A hozzárendelő függvények a fuzzy függvények.

A rezolúciós kalkulus.

Klóz:

• Literálok egy halmaza
• Ha nem tartalmaz literált, akkor üres a klóz.
• Az üres klóz kielégíthetetlen.
• Ahhoz, hogy egy klóz kielégíthető legyen, legalább egy literáljának igaznak kell lennie.

Rezolvens:

• Ha $C$ és $D$ klózok, $p$ eleme $C$ és $negált p$ eleme $D$, akkor
  • $C$ és $D$ ($p$ menti) rezolvense a
    • $(C - {p}) unió (D - {negált p} )$

Rezolúciós eljárás:

• Input: $S$ klózhalmaz.
• Output: $S$ kielégíthető vagy kielégíthetetlen.
• Algoritmus:
  • Klózokról listát vezetünk
  • Egy klózt felvehetünk, ha $S$ beli
  • Vagy két, a listán már szereplő klóz rezolvense.
• Mindaddig csináljuk ezt, míg az üres klóz rá nem kerül a listára, akkor kielégíthetetlen lesz.
• Ha már nem tudunk új klózt felvenni és nem jött ki az üres klóz, akkor kielégíthető.

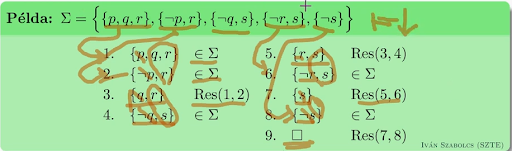
A rezolúciós algoritmus:

• Helyes:
  • Ha az algoritmus kielégíthetetlen válasszál áll meg, akkor az input S valóban kielégíthetetlen.
    • Ha azt mondom, hogy igen, akkor a válasznak tényleg igennek kellene lennie.
• Teljes:
  • Ha S kielégíthetetlen, akkor az algoritmus mindig kielégíthetetlen válasszal áll meg.
    • Ha a válasznak igennek kellene lennie, akkor én arra előbb utóbb rá is jövök.
• Viszont a rezolúció nem helyes, ha több literál mentén rezolválunk egyszerre.

A logikai program és az SLD rezolúció.

Logikai program, logikai programozás:

• Logikai program:
  • Tudást ír le, melyet a gép a neki feltett kérdésekre való válaszoláshoz felhasznál.
• Ahhoz, hogy állításokat fogalmazzunk meg, szükség van az állításban szereplő objektumok leírására, amelyet termekkel oldhatunk meg.
• Az állításaink lehetnek egyszerűek és összetettek.
  • Az egyszerű állításokat tényeknek nevezzük, leírt formában atomi formulák.
• Prolog programokban Horn-klózok szerepelhetnek.
• Horn-klóz:
  • Olyan zárt klóz, melyben véges sok negált atomi formula van, diszjunkció által összekapcsolva, és legfeljebb egy negálatlan formula.

• Prolog maga deklaratív nyelv.
  • Jelentése, leírjuk, hogy mit szeretnénk kapni.
• Működése:
  • Meg kell adni egy célklózt, ezután a program ellenőrzi, hogy a célklóz a logikai program logikai következményei közt van-e.

SLD rezolúció:

• Vegyük a P programot és egy negált állítást, ami diszjunkciók sorozatával van megadva.
• Cél, hogy a gép a B-beli diszjunkciókból tüntesse el az atomi formulákat, tehát B legyen üres, ekkor eljutott egy hamis formuláig.
• Ehhez a gép B-ben cserélgetni kezdi a formulákat, egyet kiválaszt, majd kicseréli egy vagy több negált atomi formula diszjunkciójára.
• Vagyis:
  • Kiválaszt egy negált formulát a megadott formulánkból, és kiválaszt egy klózfejet a P programból.
  • Ha ez a kettő egyezik, akkor a negált formulát kicseréli a klóz törzsére.
  • Egyesítés előtt a változókat átnevezi, hogy ne ütközzenek.

A logikai programozás alapvető módszerei.

További információk