3. Tétel: Függvények vizsgálata; Logika

Függvények szélsőértéke, függvényvizsgálat.

Függvény fogalma

Adott két halmaz, $H$ és $K$. Ha a $H$ halmaz elemeihez valamilyen egyértelmű módon hozzárendeljük a $K$ halmaznak egy-egy elemét, akkor ezt a hozzárendelést függvénynek nevezzük.

A $H$ halmazt a függvény alaphalmazának, a $K$ halmazt a függvény képhalmazának nevezzük.

A $H$ alaphalmaznak azt részhalmazát, amelyhez a képhalmaznak valamely eleme hozzá lett rendelve, a függvény értelmezési tartományának nevezzük. és $D_{f}$-fel jelöljük. $D_{f}\subseteq H$.

A képhalmaznak a függvény helyettesítési értékeit tartalmazó részét a függvény értékkészletének nevezzük és $R_{f}$-fel jelöljük. $R_{f}\subseteq K$.

A függvény tehát egyértelmű hozzárendelés az értelmezési tartomány és az értékkészlet elemei között.

Függvények szélsőértéke

A függvény azon pontjai, ahol a függvénynek minimuma vagy maximuma van.

Függvény szélsőértéke

Azt a független változót, amelyhez a legnagyobb vagy legkisebb függvényérték tartozik a függvény szélsőérték helyének nevezzük (maximum hely vagy minimum hely).

A legnagyobb vagy legkisebb függvényéréket a függvény szélsőértékének nevezzük (maximum érték vagy minimum érték).

Lokális minimum / maximum azt jelenti, hogy helyi minimum / maximum, ugyanis egy függvények lehet abszolút minimum / maximum értéke is is.

Az abszolút minimum / maximum az egyben lokális minimum / maximum is. (magyarul lokálisnál értéke kisebb / nagyobb)

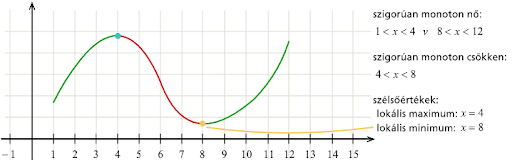
A függvény konkáv, ahol "szomorú" hangulatban van. Latin: "cavus" - angol: cave, hollow - magyar: barlang, homorú.

A függvény konvex, amikor "vidám" hangulatban van. Latin: "vexus" - angol: vaulted, arched - magyar: domború.

Jelen példa szerint:

• Konkáv 1-től 6 -ig.
• Konvex 6-tól 12 -ig.

Függvényvizsgálat

Lépései

1. Értelmezési tartomány meghatározása
2. Grafikon és a tengelyek közös pontjainak meghatározása
   • Hol metszi az x tengelyt
3. Paritás vizsgálata
   • Páros vagy páratlan vizsgálata.
   • Páros, ha szimmetrikus az y tengelyre.
   • Páratlan, ha szimmetrikus az origóra.
4. Határértékek vizsgálata
5. Monotonítás vizsgálata
6. Konvexitás vizsgálata, inflexiós pontok meghatározása
   • Inflexiós pont, ahol a függvénygörbe görbületet vált
   • Itt változik a függvény konkávból konvexbe, vagy fordítva
7. Grafikon rajzolása
8. Értékkészlet meghatározása

A legkisebb négyzetek módszere.

Legkisebb négyzetek módszere

• Egy adatsorra nagyon sok modell (egyenes) fektethető, ezek közül azt keressük, amelyik legjobban illik az adatokhoz (legjobban leírja azokat).
• Sok becslés létezik erre, de a legelterjedtebb a legkisebb négyzetek módszere.
• Gauss alkotta meg.
• Megkeressük a pontfelhő középpontját, ezzel fixáljuk az egyenes helyét!
  • X és Y változó átlaga
  • Ezen biztosan átmegy az egyenes
• Határozzuk meg az egyenes meredekségét
  • Válasszuk ki az ezen átmenő egyenesek közül azt, amelyik a legkisebb hibával jár.
• Azt a modellt keressük, amelyik legjobban illik az adatokhoz, másként megfogalmazva, ahol a legkisebb a különbség a ténylegesen mért adatok és predikált értékek között.
• A mért értékek lehetnek pozitívok és negatívak.
• Számunkra csak a mérték nagysága a lényeges, ezért a negatív előjelet eltüntetjük négyzetre emeléssel.

---

Az elsőrendű logika nyelvének szintaxisa.

Egy elsőrendű logikai nyelv ábécéje logikai és logikán kívüli szimbólumokat, továbbá elválasztójeleket tartalmaz.

A logikán kívüli szimbólumhalmaz megadható 〈Srt,Pr,Fn,Cnst〉 alakban, ahol

1. Srt nemüres halmaz, elemei fajtákat szimbolizálnak,
   • Minden $\pi \in Str$ típushoz, egy megszámlálhatóan végtelen szimbólumrendszer tartozik. Ezeket a szimbólumokat nevezzük $\pi$ fajtájú változóknak.
2. Pr nemüres halmaz, elemei predikátumszimbólumok,
   • Minden $P \in Pr$ predikátumszimbólumhoz rendelünk egy kifejezést, azaz a predikátumszimbólum alakját.
3. az Fn halmaz elemei függvényszimbólumok,
   • Minden $f \in Fn$ függvényszimbólumhoz rendelünk egy kifejezést, azaz a függvényszimbólum alakját.
4. Cnst pedig a konstansszimbólumok halmaza.
   • minden $c \in Cnst$ konstansszimbólumhoz tartozik egy $\pi \in Str$ típus.

Logikai szimbólumok:

• $\lnot$ - negáció logikai összekötő jele (not)
• $\land$ - konjukció logikai összekötő jele (and)
• $\lor$ - diszjunkció logikai összekötő jele (or)
• $\implies$ - implikáció logikai összekötő jele (implies)
• $\forall$ - univerzális kvantor (for all)
• $\exists$ - egzisztenciális kvantor (exists)

Elválasztó jelek:

• ( - nyitójel
• ) - zárójel
• , - vessző

Változók kötött és szabad előfordulása.

Egy elsőrendű logikai nyelvben azokat a kifejezéseket, amelyekben nincs individumváltozó, alapkifejezéseknek nevezzük. Így beszélhetünk alaptermekről, alapatomokról és alapformulákról. A nyelv nem alapkifejezéseiben tehát van legalább egy változó. Ugyanaz a változó természetesen egy logikai kifejezésben többször is előfordulhat. Nem alapkifejezésekre jó példák a kvantoros formulák, hisz bennük a prefixumban a kvantor után egy individuumváltozót mindenképpen le kell írni.

Vizsgáljuk most egy elsőrendű logikai nyelv kifejezéseiben a változók különböző előfordulásait. Egy kvantált formulában a kvantor a prefixumban megnevezett változó bizonyos előfordulásaira hatást fejt ki. Ez a hatás a változó-előfordulás státusának megváltozásában nyilvánul meg. Egy kifejezésben egy x változó egy adott előfordulásának kétféle státusát különböztetjük meg.

• Az x változó adott előfordulása a K kifejezésben kötött, ha egy őt megnevező kvantor hatáskörében van.
• Az x változó adott előfordulása szabad, ha nem kötött.

Egy kvantor a prefixumban megnevezett és a hatáskörében levő, ott még szabad előfordulású változókat köti.

Egy változó-előfordulás kötöttségének meghatározása:

1. A termek és az atomi formulák minden változójának minden előfordulása szabad.
2. A $\lnot A$ formulában egy változó-előfordulás pontosan akkor kötött, ha az $A$-ban van és ott kötött.
3. Az $(A∘B)$ (konjukció, diszjunkció, implikáció) formulában egy változó-előfordulás kötött, ha ez az előfordulás $A$-ban van és ott kötött, vagy $B$-ben van és ott kötött.
4. A $QxA$ formulában $x$ minden előfordulása kötött. A $Q$ kvantor teszi kötötté (köti) $x$ valamely előfordulását, ha ez az előfordulás $A$-ban még szabad. Egy az $x$-től különböző változó valamely előfordulása kötött, ha $A$-ban kötött.

A nyelv interpretációja, változókiértékelés.

info

Legyen ℒ[ V ν ] egy elsőrendű logikai nyelv. Hogy meghatározhassuk, mit jelentenek ℒ[ V ν ] termjei és formulái, meg kell adni, milyen individuumhalmazt futnak be a nyelv individuumváltozói, melyik individuumokat jelölik a konstansszimbólumok, milyen matematikai függvényeket (műveleteket) a függvényszimbólumok és mely logikai függvényeket (relációkat, predikátumokat) a predikátumszimbólumok. Ennek az információnak a rögzítését nevezzük az elsőrendű logikai nyelv egy interpretációjának.

Legyen az ℒ[ V ν ] nyelvnek ℐ egy interpretációja, az interpretáció univerzuma legyen U és jelölje V a

nyelv változóinak a halmazát. Egy olyan κ:V→U leképezést, ahol ha x π fajtájú változó, akkor κ(x)∈ U π , ℐ -beli változókiértékelésnek nevezünk.

A nyelv interpretációja:

• Egy formula kiértékeléséhez az elsőrendű logikában egy struktúrát kell megadnunk.
• Legyen ez a következő függvény négyes〈 Srt,Pr,Fn,Cnst 〉
• Konkrétan ez a struktúra 4 részből áll össze:
  1. Srt az objektumok nemüres halmaza.
  2. A Pr-ben pedig, az I interpretációs függvény minden p predikátumszimbólumhoz hozzárendel egy logikai függvényt, prédikátumot.
     • I(p) : U1 -> {0,1}
  3. Az Fn-ben pedig, az I interpretációs függvény hozzárendel minden f függvényszimbólumhoz egy matematikai függvényt.
     • I(f) : U1 -> U
  4. A Cnst-ben pedig, c függvény egy konstansszimbólumhoz rendeli az univerzum egy elemét.
     • c(x) = 3

Változókiértékelés:

• Egyen az L elsőrendű logikai nyelvnek I egy interpretációja, az interpretáció univerzuma legyen U.
• Jelölje V a nyelv változóinak halmazát.
• Egy olyan k: V -> U leképezést, ahol ha x π fajtájú változó, akkor k(x) Uπ beli individuum (egyed), az I interpretáció egy változókiértékelésének nevezzük.

Termek és formulák értéke interpretációban, változókiértékelés mellett.

info

Egy term értéke rögzített interpretációban csak a benne előforduló individuumváltozók változókiértékelésétől függ, meghatározásához elegendő csak a kérdéses term változóihoz rendelt individuumokat ismerni, azaz a term egy változókiértékelését megadni. Tehát egy n individuumváltozót tartalmazó term interpretációbeli jelentése egy olyan n -változós matematikai függvény, amely az individuumváltozók fajtáinak megfelelő individuum n -esekhez a term fajtájának megfelelő individuumokat rendel. Ha viszont a term alapterm - nem fordul elő benne változó - értéke nyilván nem függ a változókiértékeléstől. Alaptermek esetén ezért |t | ℐ,κ helyett gyakran |t | ℐ -t írunk.

info

Egy formula igazságértéke is - rögzített interpretációban - csak a benne előforduló individuumváltozók változókiértékelésétől függ, meghatározásához elegendő csak a formula változóihoz rendelt individuumokat ismerni, azaz a formula egy változókiértékelését megadni. Egy n individuumváltozót tartalmazó formula interpretációbeli jelentése egy n -változós logikai függvény (reláció), amely az individuumváltozók fajtáinak megfelelő individuum n -esekhez igazságértékeket rendel. Ha a formula zárt - nem fordul elő benne szabad változó - igazságértéke nyilván nem függ a változókiértékeléstől. Ebben az esetben ezért |C | ℐ,κ helyett gyakran most is |C | ℐ -t írunk.

Term:

• Minden változó term

Termek értéke:

• A termek objektumokat vesznek fel értékül.
• Egy t term értéke egy A struktúrában A(t) lesz.
• A változók értékét a Cnst beli c függvény mondja meg.
  • c(x) = 3
• Ha van egy f(t1,t2,..,tn) alakú függvénytermünk, akkor rekurzívan ki kell értékeljük az argumentumokat, azok mind objektumba kiértékelődnek, és ezeken az objektumokon kell kiszámolnunk az f függvény értékét.
  • Pl: f(x,f(x,y)) értéke 3 + (3 + 1) = 7, mivel
  • I(f)(n,m) := n + m, az összeadás
  • c(x) = 3, c(y) = 1

Formulák értéke:

• A formula kiértékelése a kvantorok miatt összetettebb.
• Az univerzális és egzisztenciális kvantorok hatását tekintve olyan, mint egy lokálisan deklarált változó, felülírja az x értékét a belsejében.
• Ehhez először meg kell vizsgálnunk az értékadás műveletet valahogy:
  • Ha A egy struktúra, x egy változó és a ∈ A egy objektum, akkor
    • Ax->a jelöli azt a struktúrát, amit úgy kapunk, hogy A-ból, hogy benne x default értékét a-ra állítjuk.
• Az F formula értékért A struktúrában A(F)-fel jelöljük
  • Értéke 0 vagy 1

1. Ha egy atomi formulát kell kiértékeljünk, akkor előbb értékeljük ki a termeket, aztán ezen a kapott objektum-vektoron alkalmazzuk azt a predikátumot, amit ebben a struktúrában jelölünk a p-vel.
2. Ha F = (G ∨ H), akkor A(F) = A(G) ∨ A(H), és a többi konnektívára (¬,∧,∨,⇒) hasonlóan:
   • Vagyis ha van egy konnektívánk, akkor előbb kiértékeljük a részformulákat
3. A kvantorok:
   • Ha F = ∃xG, akkor
     • A(F) := 1 ha van olyan a ∈ A objektum, amire Ax->a (G) = 1
     • A(F) := 0 egyébként
       • Tehát ∃xG akkor 1, ha felül tudjuk írni x értékét valami alkalmas a-ra úgy, hogy az így megváltoztatott Ax->a struktúrában a formula ,,belseje” magja igazzá váljon.
   • Ha pedig F = ∀xG, akkor
     • A(F) := 1, ha minden a ∈ A objektumra igaz, hogy Ax->a (G) = 1
     • A(F) := 0 egyébként

Törvény, ellentmondás, ekvivalencia, következmény.

info

Az ℒ[ V ν ] nyelv egy A formulája logikailag igaz (másképp logikai törvény), ha ℒ[ V ν ] minden ℐ interpretációjában és ℐ minden κ változókiértékelése mellett |A | ℐ,κ =i . Jelölése: ⊨A .

info

Legyen Γ az ℒ[ V ν ] nyelv formuláinak tetszőleges halmaza és B tetszőleges formulája. Azt mondjuk, hogy a B formula logikai következménye a Γ formulahalmaznak (vagy a Γ -beli formuláknak), ha minden olyan ℒ[ V ν ] -beli interpretáció és változókiértékelés, amely kielégít minden Γ -beli formulát, az kielégíti a B formulát is. Jelölése: Γ⊨B .

Törvény

• Az elsőrendű logikai nyelv egy A formulája logikai törvény, ha a nyelv minden I interpretációjában és I minden K változókiértékelése mellett |A|I,K = i.
  • Vagyis minden interpretáció minden változókiértékelést kielégít.

Ellentmondás

• Ellentmondás törvénye kimondja, hogy az A formula nem lehet egyszerre A és negált A.

Ekvivalencia

• Legyenek A és B az L nyelv tetszőleges formulái.
• Azt mondjuk, hogy A és a B elsőrendű formulák logikailag ekvivalensek, ha minden I interpretációban és a k változókiértékelés mellett
  • Jelölése: A ~ B

Következmény

• Legyen Γ egy elsőrendű nyelv formuláinak halmaza és B formula.
• B logikai következménye a Γ formulahalmaznak (vagy a Γ-beli formuláknak), ha a nyelv minden olyan interpretációja és változókiértékelése, amely kielégít minden Γ-beli formulát, az
• kielégíti a B formulát is.
• Jelölése: Γ |= B.

Normálformák, prenex formulák.

Literál

• Az atomi formulákat és a negáltjaikat nevezzük literálnak.

Elemi konjunkció

• Tekintünk minden literált, továbbá egy elemi konjunkció és egy literál konjunkcióját.

Elemi diszjunkció

• Tekintünk minden literált, továbbá egy elemi diszjunkció és egy literál diszjunkciója.

Normálformák

• Lehet:
  • Diszjunktív
    • Egy elemi diszjunkció, vagy egy konjunktív normálforma és egy elemi diszjunkció konjunkciója
  • Konjunktív
    • Egy elemi konjunkció, vagy egy diszjunktív normálforma és egy elemi konjunkció diszjunkciója.

Prenex formulák

• Egy formula prenex alakú, ha ki van igazítva és elől vannak benne a kvantorok, vagyis
  • Qx1,Qx2,...,QxnF alakú, ahol az F-ben (formula magjában) már nincs kvantor
    • Ahol Qx jelöliheti bármelyik kvantort (mindegy melyik)
      • Egzisztenciális, univerzálist

Logikai kalkulusok.

Szekventálkalkulus

• Egy olyan speciális alakú formula, amelyben az implikáció bal oldalán a formuláinak konjunkciós, a jobb oldalán a formuláinak diszjunkciós láncformulája áll.

További információk

• https://matekarcok.hu/fuggveny-fogalma-fuggvenyek-megadasa/

• https://gyires.inf.unideb.hu/KMITT/a02/ch05.html