Skip to main content

2. Tétel: Valószínűség kiszámítása; Rendező algoritmusok

Valószínűség fogalma és kiszámításának kombinatorikus módszerei (permutációk, variációk, kombinációk).​

Valószínűség fogalma​

Minél többször végzünk el egy kísérletet, egy esemény relatív gyakorisága annál jobban megközelít egy számot. Ez a szám az esemény valószínűsége.

Az esemény valószínűségét P(A)P(A)-val jelöljük.

Permutációk​

Permutáció

Egy adott nn elemű halmaz elemeinek egy ismétlés nélküli permutációjának nevezzük az nn különböző elem egy sorba rendezését.

Jelölése:

PnP_{n}

Egy nn elemű halmaz összes ismétlés nélküli permutációinak száma nn faktoriális, azaz:

Pn=n⋅(n−1)⋅(n−2)⋅…⋅2⋅1=n!P_{n} = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1 = n!
Ismétléses permutáció

Ha az nn elem között van k1,k2,…,kmk_{1}, k_{2},\ldots, k_{m} egymással megegyező elem, akkor az elemek egy sorba rendezését ismétléses permutációnak nevezzük.

Jelölése:

Pn(k1,k2,…,km)P_{n}^{(k_{1}, k_{2}, \ldots, k_{m})}

Tehát a különbség a következő: ismétlés nélküli permutáció esetén csupa különböző elemet rendezünk sorba, míg ismétléses permutáció esetén vannak megegyező elemek.

Ha egy nn elemű halmazban az nn elem között k1,k2,…,kmk_{1}, k_{2}, \ldots, k_{m} egymással megegyező elem van, és k1+k2+…+km=nk_{1} + k_{2} + \ldots + k_{m} = n, akkor ezeket az elemeket

Pn(k1,k2,…,km)=n!k1!⋅k2!⋅…⋅km!P_{n}^{(k_{1}, k_{2}, \ldots, k_{m})} = \frac{n!}{k_{1}! \cdot k_{2}! \cdot \ldots \cdot k_{m}!}

különböző módon lehet sorba rendezni. Ez a halmaz összes ismétléses permutációjának száma.

Pl: hány 5 jegyű szám írható fel 2, 2 ,2 ,7, 7 - ből?

Variációk​

Variáció

Legyen nn egymástól különböző elemünk. Ha ezekből k(k≤n)k (k \leq n) elemet kiválasztunk minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendjére tekintettel vagyunk, akkor az nn elem kk-ad osztályú ismétlés nélküli variációját kapjuk.

Jelölése:

VnkV_{n}^{k}

Ezek száma:

Vnk=n!(n−k)!=n⋅(n−1)⋅(n−2)⋅…⋅(n−k+1).V_{n}^{k} = \frac{n!}{(n-k)!}= n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n-k+1).

Pl: hányféleképpen ülhet le 5 ember közül 3 egymás mellé egy padra?

5∗4∗3=605 * 4 * 3 = 60 (ugyan az, csak másképp)

Ismétléses variáció

Legyen nn egymástól különböző elemünk. Ha ezekből kk elemet kiválasztunk minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendjére tekintettel vagyunk és ugyanazt az elemet többször is kiválaszthatjuk, akkor az nn elem kk-ad osztályú ismétléses variációját kapjuk. Jelölése:

Vnk,iV_{n}^{k,i}

Ezek száma:

Vnk,i=nkV_{n}^{k,i} = n^{k}

Kombinációk​

Kombináció

Legyen nn egymástól különböző elemünk. Ha ezekből k(k≤n)k (k \leq n) elemet kiválasztunk minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendjére nem vagyunk tekintettel, akkor az nn elem kk-ad osztályú ismétlés nélküli kombinációját kapjuk. Jelölése:

CnkC_{n}^{k}

Az n elem k-ad osztályú összes ismétlés nélküli kombinációjának száma n alatt a k:

Cnk=n⋅(n−1)⋅(n−2)⋅…⋅(n−k+1)k⋅(k−1)⋅…⋅2⋅1=n!k!⋅(n−k)!=(nk).C_{n}^{k} = \frac{n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n-k+1)}{k \cdot (k-1) \cdot \ldots \cdot 2 \cdot 1} = \frac{n!}{k! \cdot (n-k)!} = \binom{n}{k}.
Ismétléses kombináció

Legyen nn egymástól különböző elemünk. Ha ezekből kk elemet kiválasztunk minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendjére nem vagyunk tekintettel és ugyanazt az elemet többször is kiválaszthatjuk, akkor az nn elem kk-ad osztályú ismétléses kombinációját kapjuk.

Jelölése:

Cnk,iC_{n}^{k,i}

Az nn elem kk-ad osztályú összes ismétléses kombinációjának száma n+k−1n+k-1 alatt a kk:

Cnk,i=(n+k−1)!k!⋅[(n+k−1)−k]!=(n+k−1)!k!⋅(n−1)!=(n+k−1k)C_{n}^{k,i} = \frac{(n+k-1)!}{k! \cdot [(n+k-1)-k]! } = \frac{(n+k-1)!}{k! \cdot (n-1)! } = \binom{n+k-1}{k}

Feltételes valószínűség, függetlenség, Bayes-formula.​

Feltételes valószínűség​

Feltételes valószínűség

Azt mondja meg, hogy mekkora az AA esemény valószínűsége, ha tudjuk, hogy a BB esemény biztosan bekövetkezik.

Jelölése:

P(A∣B)=P(A∩B)P(B), ha P(B)>0P(A|B) = \frac{P(A\cap B)}{P(B)}, \space ha \space P(B)>0
(A felteˊve B)=P(A metszet B)P(B)(A \space feltéve \space B) = \frac{P(A \space metszet \space B)}{P(B)}

Feltételes valószínűség

Függetlenség​

Függetlenség

Hétköznapi értelemben két eseményt akkor nevezünk függetlennek, ha nincsenek egymásra befolyással, azaz az egyik bekövetkezése esetén a másik esemény bekövetkezésének az esélye sem nem nagyobb, sem nem kisebb.

Bayes-formula​

Akkor használjuk, ha egy korábban bekövetkezett esemény valószínűségét akarjuk kiszámolni egy később bekövetkezett tükrében.

Ha A és B ismert valószínűség, és ezek egyikse sem 0, valamint a P(B|A) feltételes valószínűség, akkor:

P(A∣B)=P(B∣A)P(A)P(B)P(A|B) = \frac{P(B|A)P(A)}{P(B)}

Algoritmusok lépésszáma: beszúrásos rendezés, összefésüléses rendezés, keresések lineáris és logaritmikus lépésszámmal.​

Algoritmus

Olyan eljárás (elemi lépések sorozata), melynek során a következő teljesülnek:

  • Minden lépés elvégzése után egyértelműen definiált helyzet
  • Véges sok lépés után véget ér
  • Feladatosztály tagjaira érvényes
  • Jól meghatározott objektumon, jól meghatározott műveletet végez :::

Beszúrásos rendezés​

  • Tömb elemeinek sorba rendezése.
  • Az algoritmus a k-adik lépése előtt az első k-1 elem már rendezett
  • A lépés során a k-adik elemet beszúrjuk az első k-1 elem közé az őt nagyság szerint megillető helyre, és a nála nagyobbakat eggyel eltoljuk.
  • Nagy tömbök esetén nem hatékony, mivel lépésszáma a legrosszabb és átlagos esetben is négyzetes.
  • Kis tömbökre azonban a leggyorsabb algoritmus.
  • Legjobb eset, ha a tömb rendezve van alapból.
  • Futási ideje legrosszabb esetben n * (n - 1) / 2

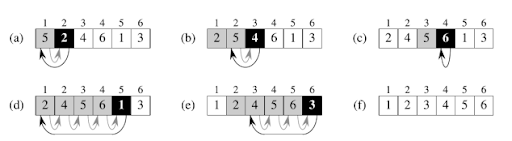
Beszuras

A rendezés során sorrendbeli hibát keresünk egy tömbben. Ennek során használhatunk lineáris, illetve bináris keresést. A kialakult sorrendtől eltérő helyen levő elemet kiemeljük, majd megkeressük a sorrendnek megfelelő helyét. Amikor a helyét megtaláltuk, akkor a közbeeső elemeket eltoljuk, majd az imént kiemelt elemet a felszabaduló helyre beszúrjuk. Ez a rendezés túl sok mozgatást igényel. :::

Összefésüléses rendezés​

  • Tömb elemeinek sorba rendezésére.
  • Oszd meg és uralkodj elven alapszik.
  • A tömböt két részre vágjuk.
  • A két résztömböt az uralkodás pontból kifolyólag ismét ketté osztjuk, és ezt addig folytatjuk (rekurzió), míg az egy elemű tömbök szintjét el nem érjük.
  • A kapott részeket összefésüli egy nagy, rendezett listává.
  • Futási ideje a gyorsrendezésével közel azonos, és a kimeneti sorozat hosszával arányos.
Összefésüléses rendezés

Az eddig ismertetett rendező algoritmusoktól eltérő, rekurzív elven működik. A c[1..n] tömb rendezése rekurzívan visszavezethető a c[1..n/2] és a c[n/2+1..n] tömbszakaszok külön-külön történő rendezésére, és az ezt követő összefésülésükre. Az általános rendez eljárást egy c[i..j] tömbszakasz rendezésére kell megírnunk. A feladat akkor triviális, ha a rendezendő tömbszakasz egyelemű (i = j).

Lineáris keresés​

  • Segítségével találhatunk meg egy tetszőleges elemet egy nem rendezett tömbben.
  • Összehasonlítjuk az elemeket.
  • A keresés véget ér, ha megtaláltuk az elemet, vagy elértünk a tömb végére.
  • Futási idő a tömb méretével lineárisan nő.
Lineáris keresés

A legegyszerűbb keresési algoritmus, amely rendezetlen tömbön dolgozik. A tömb első elemétől kezdve összehasonlítjuk a tömbelemeket a keresendő elemmel. A keresési ciklus akkor ér véget, ha valamelyik tömbelem megegyezik a keresettel, vagy, ha a tömb végére érünk. Az utóbbi esetben a keresett elem nincs a tömbben. Az algoritmus onnan kapta nevét, hogy a keresések száma, és így a futási idő, lineáris függvénye a tömb elemszámának.

Logaritmikus (bináris) keresés​

  • Segítségével egy elem rendezett tömbben való keresésére valósítható meg.
  • A keresés során minden egyes iterációban felezni lehet a résztvevő elemek számát.
  • Összehasonlítja a keresett elemet a tömb középső elemével, ha tőle kisebb a keresett elem balra megy és folytatja ezt az összehasonlítást, ha nagyobb, akkor jobbra keres.
  • Így egy n elemű tömbben O(log n) lépésben megtalálható a keresett elem, vagy megállítható a jelenlétének hiánya. (futási idő)
Logaritmikus (bináris) keresés

A logaritmikus vagy bináris keresési algoritmus rendezett tömbön működik, így az előző módszernél lényegesen gyorsabb keresést tesz lehetővé. A keresendő elemet először a tömb középső eleméhez hasonlítjuk. Ha a két elem egyezik, megtaláltuk a tömbelemet, ha nem, a keresést abban a tömbfélben folytatjuk, amelyet a középső és a keresett elem viszonya kijelöl. Ha a tömb növekvő sorrendbe rendezett és a keresendő elem nagyobb, mint a középső elem, akkor a második tömbrészben, egyébként pedig az elsőben folytatjuk a keresést. A keresést akkor fejezzük be, ha megtaláltuk a keresett tömbelemet, vagy a tömbrész elfogyott. Az összehasonlítások száma, s így a futási idő, az elemszám kettesalapú logaritmusával arányos, ami nagy elemszámok esetén lényegesen kisebb lehet, mint a lineáris keresés esetén.

Gyorsrendezés, az összehasonlítások minimális száma.​

Gyorsrendezés​

  • Tömb elemeinek sorba rendezésére.
  • Oszd meg és uralkodj elven alapszik.
  • Tömböt két részre osztja, majd ezeket rekurzívan rendezi, gyorsrendezéssel.
  • A felbontáshoz kiválaszt egy "főelemet".
  • A "főelemnél" kisebb elemeket előre, a nagyobbakat mögé mozgatja.
  • Középső elemet érdemes főelemnek választani.
  • Futási ideje n * log n.
Gyorsrendezés (quick-sort)

Ez az algoritmus is rekurzív elven működik. Szétválogatjuk az aktuális tömbszakasz (a[i..j]) elemeit a szakasz első eleme (az a[i] kulcselem) szerint, majd folytatjuk a rendezést a szakasz kulcselem előtti, illetve mögötti elemei rendezésével.

Rendezés lineáris lépésszámmal: radix rendezés, vödör rendezés.​

Radix rendezés​

  • Számjegyes rendezés
  • Azonos hosszúságú stringek rendezésére használható, ahol k a szó hossza, d az egy karakteren előforduló lehetséges jegyek, n pedig a bemenő adatok száma.
  • Futási idő k * (n + d)

Vödör / Edény rendezés​

  • Alapelve, hogy feltételezzük, hogy a rendezni kívánt tömb elemeit egy olyan algoritmus generálja, ami egyenletesen osztja el az elemeket egy adott intervallumon.
  • Rendezés során ezt az adott intervallumot felosztjuk egyenlő részintervallumokra, amelyekbe elhelyezzük az azokba beleillő elemeket.
  • Az egyes edényekben a rendezés párhuzamosan zajlik.
  • Az itt használt rendezési algoritmus szabadon választható.
  • Pl: beszúró rendezés
  • Ha a rendezés lezajlott, akkor az elemeket szekvenciálisan (egymás után) vissza kell írnunk a tömbbe.

További információk​