1. Tétel: Valószínűségi eloszlások; Adatszerkezetek

Diszkrét és folytonos valószínűségi eloszlás fogalma.

Diszkrét eloszlás

Diszkrétnek nevezzük azokat a valószínűségi változókat, ami megszámlálhatóan sok értéket vesznek fel.
Véges sok vagy végtelen, de fel tudjuk sorolni az értékeket.
Ekkor az eloszlásfüggvény lépcsőzetes lesz.
Minden számnál annyit ugrik, mint az adott szám valószínűsége.
Binomiális, Poisson

Folytonos eloszlás

Folytonosnak nevezzük azokat a valószínűségi változókat, melyek folytonos mennyiségeket mérnek.
Pl: idő
Ha az X valószínűségi változó folytonos, akkor A és B között bármilyen valós értéket felvehet.
Egyenletes, Exponenciális, Normális

Nevezetes eloszlások: binomiális, Poisson, egyenletes, exponenciális, normális.

A diszkrét eloszlású valószínűségi változó csak diszkrét, definiált értékeket vehet fel.
A folytonos eloszlású valószínűségi változó végtelen sok értéket vehet fel.

Diszkrét:

Binomiális
Geometriai
Poisson

Abszolult folytonos:

Exponenciális
Egyenletes
Normális

Binomiális eloszlás

A binomiális eloszlás egy diszkrét eloszlás.
Esetén az X korlátos, tehát van maximum értéke.
Az X valószínűségi változó
- Eseményekhez rendel hozzá számokat
- Pl: 2 balesetes nap van egy héten, X = 2
A k maga a mennyiség, amit n-ből választottunk
- Pl: 2
Az n a minta száma
- Pl: egy héten mennyi van, n = 7
A p a valószínűség
- Pl: 30 nap alatt átlag 12 van, 12/30 = 0,4

Dobjunk fel egy érmét $n$ -szer egymás után. A fejek vagy írások számának eloszlása ún. binomiális eloszlás. Az $X$ v.v. binomiális eloszlást követ, ha

P(X = k) = \binom{n}{k}p^{k}(1-p)^{n-k}, \space\space\space\space\space k = 0,1,...,n,

ahol $n \in \mathbb{N}$ és $p \in [0, 1]$ paraméterek. Jelölés: $Bi(n, p)$ .

$X$ várható értéke és szórásnégyzete:

E(X) = np, \space\space\space\space\space D(X)^{2} = np(1-p)

Mikor használunk binomiális eloszlást?

$n$ darab véletlen kísérletet végzek, mindegyik a többitől függetlenül $p$ valószínűséggel sikeres.

Legyen $X = a$ sikeres kísérletek száma. Ekkor $X$ eloszlása binomiális eloszlású $n, p$ paraméterekkel.

Például: feldobok 10 érmét, hány lesz ebből fej, egy betegség ellni gyógyszerkísérletnél hányan gyógyulnak meg, egy processzor magján hány jó mag van.

Poisson eloszlás

A poisson eloszlás egy diszkrét eloszlás.
Esetén az X nem korlátos, tehát nincs maximum értéke.
Az X valószínűségi változó
- Pl: 2 balesetek száma van egy héten, X = 2
A λ az eloszlás várható értéke
- Pl: hány baleset van egy héten, ha 30 naponta 12 baleset van.
  - 12/30 = 0,4
  - Tehát egy héten:
    - 0,4 * 7 = 2,8

Ritka események, pl. sajtóhibák száma egy lapon, meghibásodások száma egy gépnél, mazsolák egy kalácsban, eloszlásának jellemzésére szolgál. Az X v. v. Poisson eloszlást követ, ha

P(X = k) = \frac{\lambda^{k}}{k!}e^{-\lambda}, \space\space\space\space\space k = 0,1,2,...,

hol $\lambda > 0$ paraméter. Jelölés: $Po(\lambda)$ .

$X$ várható értéke és szórásnégyzete:

E(X)=\lambda, \space\space\space\space\space D^{2}(X)=\lambda

Mikor használunk Poisson eloszlást?

Amikor binomiálist használnák, de $n$ nagy $n\to \infty$ , $p$ kicsi $n\to 0$ , de a várható érték állandó $np = \lambda$

Például: Budapesten a heti tűzesetek száma (sok helyen lehet tűz, de a valószínűsége kicsi). Egy méter szövetanyagban a hibák átlagos száma (sok helyen lehet hiba, de a valószínűség kicsi). Egy webszerveren a percenkénti lekérdezések száma (sok lekérdezés van de kicsi a valószínűsége, hogy pont ezt a szervert kérdezik).

Egyenletes eloszlás

Minden érték ugyanakkora valószínűséget vesz fel.
- Pl: A az intervallum kezdete, ez a legkisebb érték, amit x felvehet. B pedig az intervallum vége, a legnagyobb érték, amit x felvehet.

Az egyik legtermészetesebb eloszlás az (egy halmazon adott) egyenletes eloszlás. Pl.: gyakran mondjuk, hogy dobjunk le egy pontot egyenletesen egy intervallumra. Ez azt jelenti, hogy egy részintervallumba esés valószínűsége arányos a részintervallum hosszával.

Az $X$ egyenletes eloszlást követ az $[a, b]$ intervallumon, ha sűrűségfüggvénye:

f(x)= \left\{\begin{matrix} \frac{1}{b-a} & ha\space a<x<b \\ 0 & egyébként \\ \end{matrix}\right.

Jelölés: $Uni(a, b)$ .

$X$ várható értéke és szórásnégyzete:

E(X) = \frac{a+b}{2}, \space\space\space\space\space D^{2}(X) = \frac{( b -a )^{2}}{12}

Mikor használunk Egyenletes eloszlást?

Ha egy véletlen érték biztosan $a$ és $b$ érték közé esik, de semmilyen más információ nem tudott róla, akkor $[a, b]$ -n egyenletes eloszlást kell használni. Jelölés: $Uni(a, b)$ .

Például: Világutazó barátom részegen felhív és mikor fut be a hívás egyneletes $[0, 24]$ -en. Egy $1$ méter hosszú kötélnek van piros és kék vége. Tökéletesen összeragasztom a két végét, hogy egy kört kapjak, majd megpörgetem ezt a kört egy olló nyitott szárai között, majd elcsattintom az ollót. Újra szétszedem a kötelet az összeragasztásnál, akkor a piros végű darab hossza egyenletes eloszású $[0, 1]$ -en.

Eloszlásfüggvénye:

F(x)=\left\{\begin{matrix} 0 & x \leq a \\ \frac{x-a}{b-a} & a<x\leq b \\ 1 & b<x \\ \end{matrix}\right.

$X$ várható értéke és szórásnégyzete:

E(X) = \frac{a+b}{2}, \space\space\space\space\space D^{2}(X) = \frac{( b -a )^{2}}{12}

Exponenciális eloszlás

Az exponenciális eloszlás élettartamok, várakozási idők, általában egy esemény bekövetkezéséig eltelő véletlen időtartamok hosszának jellemzésekor szokott előkerülni.
Ezzel összefügg, hogy értéke csak pozitív lehet.
Legfontosabb tulajdonsága az örökifjúság.
Exponenciális eloszlásnak nincs ,,memóriája”, a további várakozási esélyeket nem befolyásolja az, hogy már valamennyi időt vártunk.

Mikor használunk exponenciális eloszlást?

Olyan időintervallum hosszára, amikor várok valaminek a bekövetkeztére sokszor használunk exponenciális eloszlást.

Például: Egy telefonközpontban két hívás közt eltelt idő. Egy egyszerű alkatrész élettartama. Nukleáris bomlás

Az exponenciális eloszlás eloszlásfüggvénye:

F(x) = \left\{\begin{matrix} 0 & ha\space x\leq 0 \\ 1-e^{-\lambda x} & ha\space 0<x \\ \end{matrix}\right.

$X$ várható értéke és szórása:

E(X) = \frac{1}{\lambda}, \space\space\space\space\space D(X) = \frac{1}{\lambda}

Normális eloszlás

A normális eloszlásnak van sűrűségfüggvénye (alakja haranggörbe), viszont eloszlásfüggvénye nincs.
Ezért, bevezetünk egy speciális normális eloszlást, melynek a várható értéke 0, a szórása pedig 1.
Ezt standard normális eloszlásnak nevezzük.
Standard normális eloszlás sűrűségfüggvénye a Gauss-görbe.
Jele:
- Φ (fi)

A természetben egyik leggyakrabban eloforduló eloszlás, az alakja kapcsán gyakran harang-görbe eloszlásról beszélnek. Ennek elméleti alapja a központi határeloszlás tétel, melyet szokás úgy interpretálni, hogy sok független, azonos eloszlású kis hatás összesítése (megfelelő normálás után) normális eloszlást eredményez.

Az $X$ normális eloszlást követ, ha sűrűségfüggvénye:

f(x) = \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(x-m)^{2}}{2\sigma ^{2}}}, \space\space\space\space\space x\in\mathbb{R}

ahol $m \in\mathbb{R}$ és $\sigma > 0$ paraméterek. Jelölés: $N (m, \sigma^{2})$ .

$X$ várható értéke és szórásnégyzete (azaz a paraméterek jelentése):

E(X) = m,\space\space\space\space\space D^{2}(X)=\sigma^{2}

Az $N(0, 1)$ eloszlást standard normális eloszlásnak nevezik.

Adatszerkezetekkel kapcsolatos alapfogalmak

A valós világ rendszereinek alkotóelemei az egyedek, melyek tulajdonságokkal, és viselkedésmóddal rendelkeznek.

tulajdonság statikus jellemző

viselkedésmód dinamikus jellemző, az egyedek egymáshoz való kapcsolatát jellemzi

Modellalkotás: lényeges jellemzők kiemelése, lényegtelenek figyelmen kívül hagyása

A modellezés lényege: absztrakció

Azon tulajdonságok, melyek lehetőleg minél több egyednél megtalálhatóak: az egyedek karakterisztikus tulajdonságai
Viselkedésmód elemek

A modell nem egyedi dolgokkal, hanem ezen dolgok absztrakt osztályaival foglalkozik.

Informatikában:

tulajdonság: adat
viselkedésmód: program

Az adatelemek lehetnek egyszerűek (atomiak) és összetettek.

Minden adatelem rendelkezik valamilyen értékkel

Absztrakció (logikai és fizikai szint)

Logikai szint:

Az adatelemek között jól meghatározott kapcsolatrendszervan. Az adatelemek és a közöttük lévő kapcsolatok definiáljáka logikai (absztrakt) adatszerkezetet. Független hardvertől,szoftvertől.
absztrakt adatszerkezetek, melyek függetlenek a platformtól, a számítőgéptől

Fizikai szint:

Fizikai adatszerkezet (társzerkezet): adatszerkezet az operatívtárban vagy periférián (háttértáron).
hardver + szoftveraz adatok tárolására szolgáló hely
- memória (tár)
- háttértároló (állományok)

Absztrakt adatszerkezetek (homogén-heterogén, statikus-dinamikus, struktúra, műveletek)

Lehetséges csoportosítási szempontok:

Milyen az adatszerkezet elemeinek a típusa?

homogén
heterogén

Változhat-e az adatszerkezet elemeinek száma?

statikus
dinamikus

Milyen kapcsolatban állnak egymással az adatelemek az adatszerkezetben?

Egy homogén adatszerkezet lehet
- struktúra nélküli
- asszociatív
- szekvenciális
- hierarchikus
- hálós
A heterogén adatszerkezeteket nem csoportosítjuk ilyenszempont alapján.

Absztrakt adatszerkezetekkel végezhető műveletek:

Létrehozás
Módosítás
- bővítés
- törlés (fizikai, logikai)
- csere
Rendezés
Keresés
Elérés
Bejárás
Feldolgozás

Ábrázolási (tárolási) módok

Ábrázolás alatt az adatszerkezet memóriában való megjelenési formáját értjük. Ez minden adatszerkezet esetén lehet

folytonos (vektorszerű)
szétszórt (láncolt)

Az adatelemek számára tárhelyeket foglalunk a memóriában. Egy tárhely mindig egy bájtcsoportot jelent, amely egy adatelem értékét tárolja, illetve szerkezetleíró információkat is hordozhat.

Folytonos (vektorszerű) tárolás

Egy tárhelyen egy adatelem értékét tároljuk. A tárhelyek amemóriában folytonos, összefüggő tárterületet alkotnak, atárhelyek mérete azonos.

Előnye:

közvetlen elérés, a kezdőcím és az egy adatelemheztartozó tárhely méretének ismeretében
a csere m űvelete könnyen megvalósítható
hatékony rendező algoritmusok (pl. gyorsrendezés)
hatékony kereső algoritmusok (pl. bináris keresés)

Hátránya:

nem segíti a bővítés és a fizikai törlés m ű veleténekvégrehajtását

Szétszórt (láncolt) tárolás

Egy tárhelyen egy adatelem értékét (adatrész) és legalább egy mutató értékét (mutatórész) tároljuk. A mutatók értékei memóriacímek lehetnek, amelyek megmondják az adatelem rákövetkezőinek tárbeli helyét. A tárhelyek mérete nem szükségképpen azonos, elhelyezkedésük a memóriában tetszőleges.

A szétszórt ábrázolási mód alapvető fajtái:

egyirányban láncolt lista
cirkuláris lista
kétirányban láncolt lista
multilista

Elemi adatszerkezetek: lista, verem, sor.

Lista

Dinamikus, homogén, szekvenciális adatszerkezet.

Jelölések

Üres lista: q = []
Nem üres lista: q = [x1,x2…,xn]
Lista feje: x1
Lista vége: xn
Lista farka: [x2,...,xn]
Lista hossza: n

Alapműveletek

Hozzáférés, elérés: közvetlen q[i] = n
Részlista képzés
Konkatenáció, egyesítés

Listával végezhető műveletek

Bővítés
- Bárhol bővíthető
- Bővítéskor részlistákat képzünk, és konkatenáljuk
Törlés
- Megvalósítható fizikai törlés
- Részlistákat képzünk, és a törlendő elemet kihagyjuk
Csere
- Bármelyik elem cserélhető
- Részlistaképzés
Rendezés
- Értelmezhető
Keresés
- értelmezhető
Elérés
- Soros vagy közvetlen
Bejárás
- értelmezhető
Feldolgozás
- Alapműveletek segítségével

Szélső elemekkel végezhető műveletek

Access head
- Első elem elérése
Push
- Bővítés az első elem előtt
Pop
- Első elem törlése
Access end
- Utolsó elem elérése
Inject
- Bővítés az utolsó elem után
Eject
- Az utolsó elem törlése

Ábrázolása

Folytonos reprezentáció:

Vektorral
Lista elemei egy tömbben vannak eltárolva egymás után.
Könnyen bejárható.
Egy új elem a lista végére kerül.
Ha a közepére szúrunk be, az mozgatással jár, ahogy a törlés szintén.

Szétszórt reprezentáció:

Láncolt listával
Beszúrás:
- Lista elejére, végére, aktuális elem után, elé
Törlés:
- Lista eleje, vége, aktuális elem

Tömb ábrázolása

Verem

Speciális lista adatszerkezet. Csak a verem tetejére lehet betenni, illetve onnan kivenni. Az utoljára betett elem a verem tetejére kerül. Az elsőnek betett elem a verem aljára.

Végezhető műveletek:

Létrehozás
- Üres verem létrehozása
Bővítés
- Új elem bevitele az utoljára betett elem fölé (PUSH)
Csere
- nincs
Törlés
- Fizikai, verem tetején (POP)
Rendezés, keresés, bejárás
- Nem értelmezett
Elérés
- Felső elemet közvetlenül, többit sehogyan
Feldolgozás
- Last in first out (LIFO adatszerkezet)
- utolsóként értelmező adatelem feldolgozása először.

Ábrázolás:

Folytonos reprezentáció:

A veremmutató mindig a verem tetején lévő elemet indexeli.
Ha a veremmutató értéke 0, a verem üres.
Ha a veremmutató értéke n, a verem tele van.

Verem Folytonos

Szétszort reprezentáció:

Egyirányban láncolt listával
- A fej mutató mindig a verem tetején lévő elemre mutat.
- Ha a fejnek NIL az értéke, a verem üres.

Verem Szétszort

Sor

Specialis lista adatszerkezet

Alapműveletei

Első elemhez történő hozzáférés
- Access head
Bővítés az utolsó elem mögé
- Put (INJECT)
Első elem törlése
- Get (POP)

Sorral végezhető műveletek

Létrehozás
- Üres sor
Bővítés
- Utolsó elem mögé
Csere
- nincs
Törlés
- Fizikai, az első elemet
Rendezés, keresés, bejárás
- Nem értelmezett
Elérés
- Az első elemet közvetlenül, a többit sehogyan sem
Feldolgozás
- First in First out (FIFO) adatszerkezet.
- Az elsőként érkező elemet dolgozzuk fel először

Ábrázolás:=

Folytonos reprezentáció:

Sor első helye rögzített, mindig az 1. Indexű tárhely a vektorban.
A v mutató a sor utolsó elemét indexeli.
Üres a sor, ha v = 0.
Tele van a sor, ha v = n.
Új elemet a v + 1 pozícióba helyezünk.
Törléskor csúsztatjuk az elemeket.

Szétszórt reprezentáció:

Egyirányban láncolt listával, két segédmutatóval (első, utolsó)
Elérni és feldolgozni az első mutató által hivatkozott elemet tudjuk.
Bővíteni pedig az utolsó mutató által hivatkozott elem mögé tudunk.
A sor üres, ha mindkét segédmutató értéke NIL.

Halmaz, multihalmaz, mátrix.

Halmaz

Struktúra nélküli, homogén és dinamikus adatszerkezetek. Minden eleme különböző. Adatszerkezetben lévő elemek között nincs kapcsolat (ezért struktúra nélküli.)

Alapműveletei

Eleme
Uniója
Metszet
Különbség

Hagyományos műveletek

Adatfeldolgozás
- a halmaz alapműveleteinek segítségével
Csere
- Nincs
Rendezés, keresés, elérés, bejárás
- nem értelmezettek
Törlés
- csak fizikai, különbségképzéssel
Bővítés
- unió képzéssel
Reprezentáció
- Karakterisztikus függvény segítségével
- Elemeit sorba rendezzük, és mindegyikhez hozzárendelünk egy-egy bit méretű tárterületet.
- Az adott értékű adatelemhez tartozó bit fogja jelezni, hogy az adatelem benne van-e a halmazban (1) vagy nem (0).

Multihalmaz

Struktúra nélküli, homogén, dinamikus adatszerkezet. Elemek között nincs kapcsolat. Több azonos elem is előfordulhat.

Alapműveletei

Alapműveletei halmazéval megegyezőek

Hagyományos műveletek

Hagyományos műveletek hasonlóak a halmazokéhoz

Reprezentációja

Karakterisztikus függvénnyel történik
Elemeit sorba rendezzük, mindegyikhez hozzárendelünk egy tárterületet.
Általában 1 byte-ot.
A tárhelyen az adott értékű elemek előfordulásainak számát tároljuk.

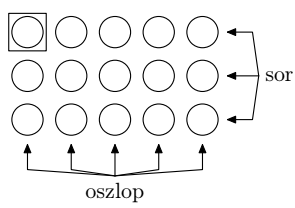
Mátrix

Kétdimenziós tömb

Mátrix

Végezhető műveletek

Létrehozás
- Rögzítjük a dimenziót és az indextartományokat.
- Ezzel egyidőben meghatározzuk a tömb elemszámát is
- A szerkezet kialakításával párhuzamosan elemeket is elhelyezhetünk a tömbben.
Bővítés
- Nincs, ugyanis a tömb statikus
Csere
- Bármely létező elem értékét felülírhatjuk egy új értékkel
- Elhelyezhetünk elemet oda, ahová létrehozáskor nem tettünk
Törlés
- Csak logikai
Rendezés
- Egydimenziós tömböknél
Keresés
- Reprezentációfüggő művelet
Bejárás
- Reprezentációfüggő művelet
Feldolgozás
- Alapja a közvetlen elérés
Leképezés:
- Történhet sorfolytonosan vagy oszlopfolytonosan

Négyzetes (kvadratikus) mátrixok.

Az olyan négyzetes mátrixot, amelynek főátlója alatt csupa 0 elem található, felsőháromszög-mátrixnak nevezzük.
Az olyan négyzetes mátrixot, amelynek főátlója fölött lévő elemek mindegyikének értéke 0, akkor alsóháromszög-mátrixról beszélünk.

Fák ábrázolása, keresések, bejárások, törlés, beszúrás.

Hierarchikus adatszerkezet

Minden adatelemének - egyet kivéve - pontosan egy megelőzője, és tetszőleges számú (akár 0) rákövetkezője lehet.

Pl: fa

Fák ábrázolása

Homogén, dinamikus, hierarchikus adatszerkezet.

Részei:

Csúcs, csomópont

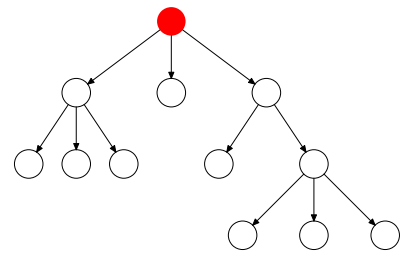
Gyökérelem

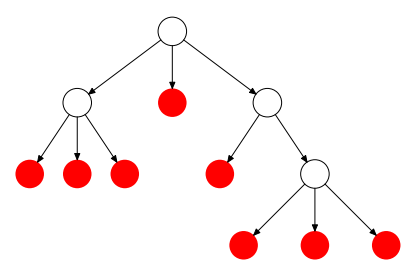
Levélelem

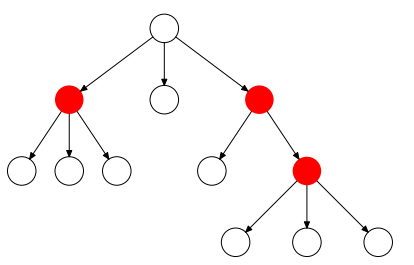
Közbenső elem

Él

Út

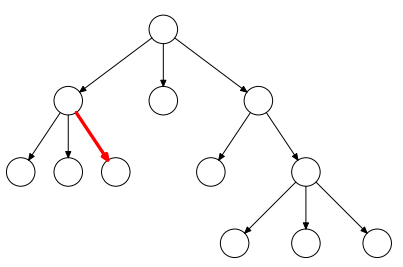
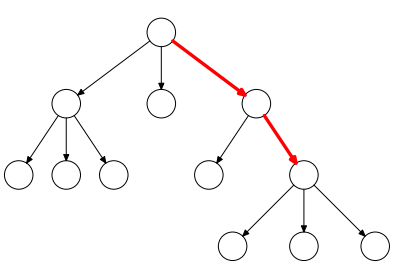
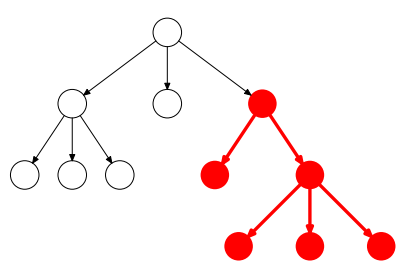
Részfa

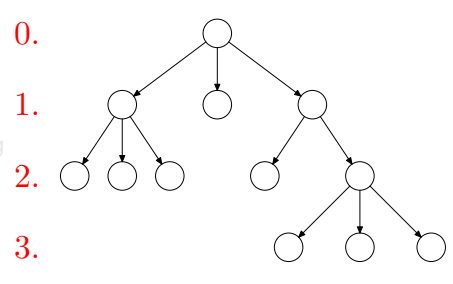
Szint

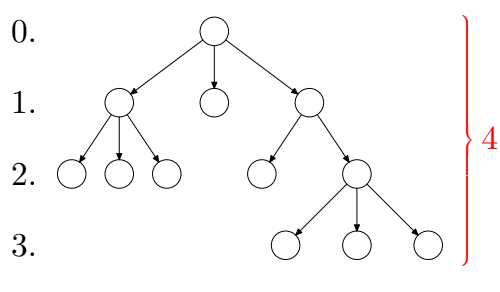
Magasság

Bináris fa

Olyan fa, melyben minden adatelemnek legfeljebb két rákövetkezője van.

Szigorú értelemben vett bináris fa

Olyan bináris fa, ahol minden adatelemnek 0 vagy 2 rákövetkezője van.

Bináris keresőfa

Olyan rendezett bináris fa, melyben az adatelemek mindegyike rendelkezik egy kulccsal, és minden adatelemre igaz, hogy az adatelem bal oldali részfájában lévő elemek kulcsai kisebbek, a jobb oldali részfájában lévő elemek kulcsai pedig nagyobbak az elem kulcsánál.

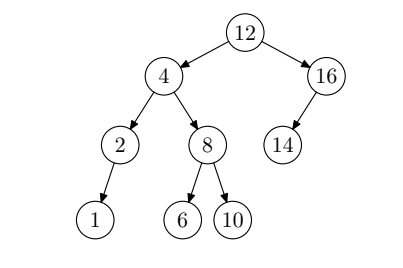
Bináris keresőfa

Műveletek

Létrehozás
- Üres fa
Bővítés
- Egy elemmel vagy részfával
Törlés
- Részfát vagy elemet
Bejárás
- Olyan algoritmus, melynek segítségével a bináris fa elemeit leképezzük egy sorra
- Preorder, inorder, postorder módon.

Reprezentációja

Folytonos
- Vektor segítségével
Szétszórt
- Láncolt lista segítségével

Bejárások

Preorder bejárás

Ha a bejárandó fa üres, az algoritmus véget ér.
Dolgozzuk fel a gyökérelemet.
Járjuk be a gyökérelem bal oldali részfáját preorder módon.
Járjuk be a gyökérelem jobb oldali részfáját preorder módon.

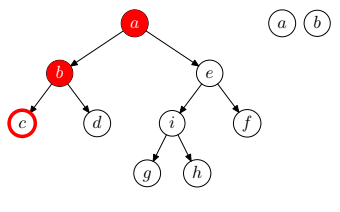
Preorder

Inorder bejárás

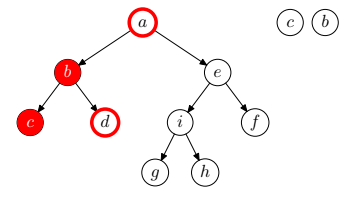
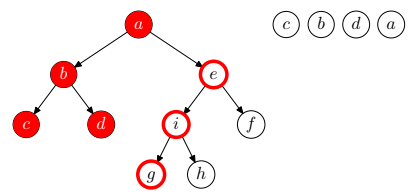
Ha a bejárandó fa üres, az algoritmus véget ér.
Járjuk be a gyökérelem bal oldali részfáját inorder módon.
Dolgozzuk fel a gyökérelemet
Járjuk be a gyökérelem jobb oldali részfáját inorder módon.

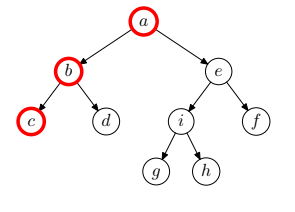
Inorder 1

Inorder 2

Inorder 3

Postorder bejárás

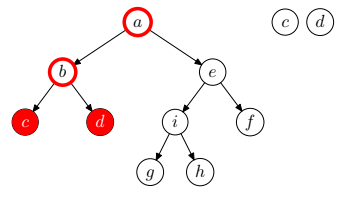
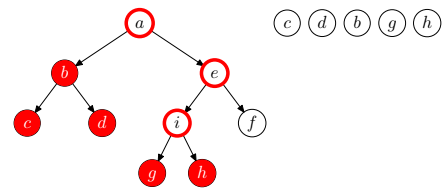
Ha a bejárandó fa üres, az algoritmus véget ér.
Járjuk be a gyökérelem bal oldali részfáját postorder módon.
Járjuk be a gyökérelem jobb oldali részfáját postorder módon.
Dolgozzuk fel a gyökérelemet.

Postorder 1

Postorder 2

Keresések

Keresés bináris fában

Bináris keresőfában az elemek rendezettek, bal oldalon a kisebbek, jobb oldalon a nagyobbak, így a keresés elég egyszerű, vizsgáljuk a gyökért, majd ha nagyobb a keresett elem jobbra, ha kisebb balra indulunk el, rekurzívan.

Törlés

Törlés bináris fából

Ha üres a fa, akkor nem tudunk törölni, és ezzel az algoritmus sikertelenül véget ér.
Összehasonlítjuk a gyökérelem értékét a törlendő elemmel.
Ha a törlendő elem kisebb a gyökérelemnél, akkor a gyökérelem bal oldali részfájából töröljük a törlendő elemet.
Ha a törlendő elem nagyobb a gyökérelemnél, akkor a gyökérelem jobb oldali részfájából töröljük a törlendő elemet.
Ha a két elem egyenlő, akkor megnézzük, hogy a gyökérelemnek hány rákövetkezője van.
Ha a gyökérelemnek egy rákövetkezője sincs (azaz levélelem), akkor egyszerűen törölhető.
Ha a gyökérelemnek egy rákövetkezője van, akkor felülírjuk a gyökérelemet azzal a rákövetkező elemmel (azaz egy szinttel feljebb csúsztatjuk a gyökérelem nem üres részfáját).
Ha a gyökérelemnek két rákövetkezője van, akkor a gyökérelem értékét felülírjuk a gyökérelem bal oldali részfája legjobboldalibb elemének az értékével, majd a gyökérelem bal oldali részfájából töröljük ezt a legjobboldalibb elemet.
Ezzel az algoritmus sikeresen véget ér.

Beszúrás

Bináris keresőfa bővítése:

Ha üres a fa, akkor a beszúrandó elem lesz a fa egyetlen eleme (levéleleme)
Összehasonlítjuk a gyökérelem értékét a beszúrandó elemmel.
- Ha a két elem egyenlő, akkor a beszúrandó elemet nem helyezhetjük el a fában, és ezzel az algoritmus sikertelenül véget ér.
- Ha a beszúrandó elem kisebb a gyökérelemnél, akkor a gyökérelem bal oldali részfáját bővítjük a beszúrandó elemmel.
- Egyébként a gyökérelem jobb oldali részfáját bővítjük a beszúrandó elemmel.

1. Tétel: Valószínűségi eloszlások; Adatszerkezetek

Diszkrét és folytonos valószínűségi eloszlás fogalma.​

Nevezetes eloszlások: binomiális, Poisson, egyenletes, exponenciális, normális.​

Binomiális eloszlás​

Mikor használunk binomiális eloszlást?​

Poisson eloszlás​

Mikor használunk Poisson eloszlást?​

Egyenletes eloszlás​

Mikor használunk Egyenletes eloszlást?​

Exponenciális eloszlás​

Mikor használunk exponenciális eloszlást?​

Normális eloszlás​

Adatszerkezetekkel kapcsolatos alapfogalmak​

Absztrakció (logikai és fizikai szint)​

Absztrakt adatszerkezetek (homogén-heterogén, statikus-dinamikus, struktúra, műveletek)​

Ábrázolási (tárolási) módok​

Folytonos (vektorszerű) tárolás​

Szétszórt (láncolt) tárolás​

Elemi adatszerkezetek: lista, verem, sor.​

Lista​

Verem​

Sor​

Halmaz, multihalmaz, mátrix.​

Halmaz​

Multihalmaz​

Mátrix​

Fák ábrázolása, keresések, bejárások, törlés, beszúrás.​

Fák ábrázolása​

Bejárások​

Keresések​

Törlés​

Beszúrás​

További információk​

Diszkrét és folytonos valószínűségi eloszlás fogalma.

Nevezetes eloszlások: binomiális, Poisson, egyenletes, exponenciális, normális.

Binomiális eloszlás

Mikor használunk binomiális eloszlást?

Poisson eloszlás

Mikor használunk Poisson eloszlást?

Egyenletes eloszlás

Mikor használunk Egyenletes eloszlást?

Exponenciális eloszlás

Mikor használunk exponenciális eloszlást?

Normális eloszlás

Adatszerkezetekkel kapcsolatos alapfogalmak

Absztrakció (logikai és fizikai szint)

Absztrakt adatszerkezetek (homogén-heterogén, statikus-dinamikus, struktúra, műveletek)

Ábrázolási (tárolási) módok

Folytonos (vektorszerű) tárolás

Szétszórt (láncolt) tárolás

Elemi adatszerkezetek: lista, verem, sor.

Lista

Verem

Sor

Halmaz, multihalmaz, mátrix.

Halmaz

Multihalmaz

Mátrix

Fák ábrázolása, keresések, bejárások, törlés, beszúrás.

Fák ábrázolása

Bejárások

Keresések

Törlés

Beszúrás

További információk